Optimal Baseball#
This chapter is available as a Jupyter notebook where you can read the text, run the code, and work on the exercises. Click here to access the notebooks: https://allendowney.github.io/ModSimPy/.
In the previous chapter we developed a model of the flight of a baseball, including gravity and a simple version of drag, but neglecting spin, Magnus force, and the dependence of the coefficient of drag on velocity.
In this chapter we apply that model to an optimization problem. In general, optimization is a process for improving a design by searching for the parameters that maximize a benefit or minimize a cost. For example, in this chapter we’ll find the angle you should hit a baseball to maximize the distance it travels. And we’ll use a new function, called maximize_scalar that searches for this angle efficiently.
The Manny Ramirez Problem#
Manny Ramirez is a former member of the Boston Red Sox (an American baseball team) who was notorious for his relaxed attitude and taste for practical jokes. Our objective in this chapter is to solve the following Manny-inspired problem:
What is the minimum effort required to hit a home run in Fenway Park?
Fenway Park is a baseball stadium in Boston, Massachusetts. One of its most famous features is the “Green Monster”, which is a wall in left field that is unusually close to home plate, only 310 feet away. To compensate for the short distance, the wall is unusually high, at 37 feet (see http://modsimpy.com/wally).
Starting with params from the previous chapter, I’ll make a new Params object with two additional parameters, wall_distance and wall_height, in meters.
feet_to_meter = (1 * units.feet).to(units.meter).magnitude
params = params.set(
wall_distance = 310 * feet_to_meter,
wall_height = 37 * feet_to_meter,
)
show(params)
| value | |
|---|---|
| x | 0.0000 |
| y | 1.0000 |
| angle | 45.0000 |
| speed | 40.0000 |
| mass | 0.1450 |
| diameter | 0.0730 |
| C_d | 0.3300 |
| rho | 1.2000 |
| g | 9.8000 |
| t_end | 10.0000 |
| wall_distance | 94.4880 |
| wall_height | 11.2776 |
The answer we want is the minimum speed at which a ball can leave home plate and still go over the Green Monster. We’ll proceed in the following steps:
For a given speed, we’ll find the optimal launch angle, that is, the angle the ball should leave home plate to maximize its height when it reaches the wall.
Then we’ll find the minimum speed that clears the wall, given that it has the optimal launch angle.
Finding the Range#
Suppose we want to find the launch angle that maximizes range, that is, the distance the ball travels in the air before landing. We’ll use a function in the ModSim library, maximize_scalar, which takes a function and finds its maximum.
The function we pass to maximize_scalar should take launch angle in degrees, simulate the flight of a ball launched at that angle, and return the distance the ball travels along the \(x\) axis.
def range_func(angle, params):
params = params.set(angle=angle)
system = make_system(params)
results, details = run_solve_ivp(system, slope_func,
events=event_func)
x_dist = results.iloc[-1].x
print(angle, x_dist)
return x_dist
range_func makes a new System object with the given value of
angle. Then it calls run_solve_ivp and
returns the final value of x from the results.
We can call range_func directly like this:
range_func(45, params)
45 99.31829628352207
99.31829628352207
With launch angle 45°, the ball lands about 99 meters from home plate.
Now we can sweep a sequence of angles like this:
angles = linspace(20, 80, 21)
sweep = SweepSeries()
for angle in angles:
x_dist = range_func(angle, params)
sweep[angle] = x_dist
Here’s what the results look like.
sweep.plot()
decorate(xlabel='Launch angle (degrees)',
ylabel='Range (m)')
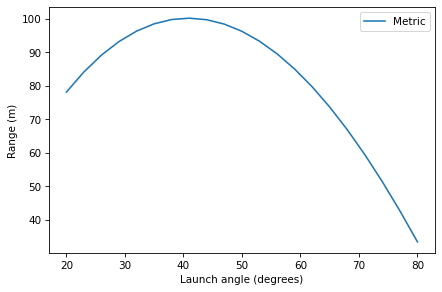
It looks like the range is maximized when the initial angle is near 40°.
We can find the optimal angle more precisely and more efficiently using maximize_scalar, like this:
res = maximize_scalar(range_func, params, bounds=[0, 90])
0 17.468795355645696
34.37694101250946 98.06996498016366
55.62305898749054 90.03182421721928
21.246117974981075 80.72039493627986
41.173855871044005 100.1200188931698
40.980120907838035 100.12368377099199
40.882137319070246 100.1241700443184
40.87925420124324 100.12417043309694
40.87928713865314 100.12417043314977
40.879291078324286 100.12417043314917
40.879283198981994 100.12417043314895
The first parameter is the function we want to maximize. The second is the range of values we want to search; in this case, it’s the range of angles from 0° to 90°.
The return value from maximize_scalar is an object that contains the
results, including x, which is the angle that yielded the maximum
range, and fun, which is the range when the ball is launched at the optimal angle.
res
fun: 100.12417043314977
message: 'Solution found.'
nfev: 10
nit: 10
status: 0
success: True
x: 40.87928713865314
res.x, res.fun
(40.87928713865314, 100.12417043314977)
For these parameters, the optimal angle is about 41°, which yields a range of 100 m. Now we have what we need to finish the problem; the last step is to find the minimum velocity needed to get the ball over the wall. In the exercises at the end of the chapter, I provide some suggestions. Then it’s up to you!
Summary#
This chapter introduces a new tool, maximize_scalar, that provides an efficient way to search for the maximum of a function. We used it to find the launch angle that maximizes the distance a baseball flies through the air, given its initial velocity.
If you enjoy this example, you might be interested in this paper: “How to hit home runs: Optimum baseball bat swing parameters for maximum range trajectories”, by Sawicki, Hubbard, and Stronge, at http://modsimpy.com/runs.
In the next chapter, we start a new topic: rotation!
Exercises#
This chapter is available as a Jupyter notebook where you can read the text, run the code, and work on the exercises. You can access the notebooks at https://allendowney.github.io/ModSimPy/.
Exercise 1#
Let’s finish off the Manny Ramirez problem:
What is the minimum effort required to hit a home run in Fenway Park?
Although the problem asks for a minimum, it is not an optimization problem. Rather, we want to solve for the initial speed that just barely gets the ball to the top of the wall, given that it is launched at the optimal angle.
And we have to be careful about what we mean by “optimal”. For this problem, we don’t want the longest range; we want the maximum height at the point where it reaches the wall.
If you are ready to solve the problem on your own, go ahead. Otherwise I will walk you through the process with an outline and some starter code.
As a first step, write an event_func that stops the simulation when the ball reaches the wall at wall_distance, which is a parameter in params.
Test your function with the initial conditions.
Show code cell content
# Solution
def event_func(t, state, system):
x, y, vx, vy = state
return x - system.wall_distance
Show code cell content
# Solution
system = make_system(params)
event_func(0, system.init, system)
-94.48799999999999
Next, write a function called height_func that takes a launch angle, simulates the flight of a baseball, and returns the height of the baseball when it reaches the wall.
Test your function with the initial conditions.
Show code cell content
# Solution
def height_func(angle, params):
params = params.set(angle=angle)
system = make_system(params)
results, details = run_solve_ivp(system, slope_func,
events=event_func)
height = results.iloc[-1].y
return height
Show code cell content
# Solution
height_func(40, params)
6.661045303535705
Now use maximize_scalar to find the optimal angle. Is it higher or lower than the angle that maximizes range?
Show code cell content
# Solution
res = maximize_scalar(height_func, params, bounds=[0, 90])
res
fun: 7.217049532932801
message: 'Solution found.'
nfev: 13
nit: 13
status: 0
success: True
x: 43.105080979149434
Show code cell content
# Solution
res.x, res.fun
(43.105080979149434, 7.217049532932801)
The angle that maximizes the height at the wall is a little higher than the angle that maximizes range.
Now, let’s find the initial speed that makes the height at the wall exactly 37 feet, given that it’s launched at the optimal angle.
This is a root-finding problem, so we’ll use root_scalar.
Write an error function that takes a speed and a System object as parameters. It should use maximize_scalar to find the highest possible height of the ball at the wall, for the given speed. Then it should return the difference between that optimal height and wall_height, which is a parameter in params.
Show code cell content
# Solution
def error_func(speed, params):
params = params.set(speed=speed)
print(params.speed)
res = maximize_scalar(height_func, params, bounds=[0, 90])
return res.fun - params.wall_height
Test your error function before you call root_scalar.
Show code cell content
# Solution
error_func(40, params)
40
-4.060550467067197
Show code cell content
# Solution
error_func(50, params)
50
30.230189540329683
Then use root_scalar to find the answer to the problem, the minimum speed that gets the ball out of the park.
Show code cell content
# Solution
bracket = [30, 50]
res = root_scalar(error_func, params, bracket=bracket)
30
30.0
50.0
42.95327159575888
41.030931458411445
41.039294634028856
41.037242669296155
Show code cell content
# Solution
res
converged: True
flag: 'converged'
function_calls: 6
iterations: 5
root: 41.039294634028856
Show code cell content
# Solution
min_speed = res.root
min_speed
41.039294634028856
And just to check, run error_func with the value you found.
Show code cell content
# Solution
error_func(min_speed, params)
41.039294634028856
0.0010039392295357885
Under the Hood#
maximize_scalar uses a SciPy function called minimize_scalar, which provides several optimization methods. By default, it uses bounded, a version of Brent’s algorithm that is safe in the sense that it always uses values within the bounds you provide (including both ends).
You can read more about it at http://modsimpy.com/minimize).