Quiz 6#

BEFORE YOU START THIS QUIZ:

Click on “Copy to Drive” to make a copy of the quiz,
Click on “Share”,
Click on “Change” and select “Anyone with this link can edit”
Click “Copy link” and
Paste the link into this Canvas assignment.

This quiz is open notes, open internet.

You can ask for help from the instructor, but not from anyone else.
You can use code you find on the internet, but if you use more than a couple of lines from a single source, you should attribute the source.

A tree of sequences#

Suppose you have a large number of DNA sequences, represented using strings containing the characters A, C, G, and T, which are the bases that make up DNA.

One way to store these sequences is in a tree where each node has four children, one for each base. Here’s a class definition for such a node.

class Node:
    def __init__(self):
        self.children = [None, None, None, None]
        self.end = False
        
    def __repr__(self):
        return f'Node({self.end}, {self.children})'

The instance variables are:

children, which is a list of four Node objects, where None indicates that a child is missing.
end: which is a bool that indicates whether this Node represents the end of a sequence.

I’ll use the following dictionary to map from each base to its index in the list of children.

index_map = dict(A=0, C=1, G=2, T=3)
index_map

{'A': 0, 'C': 1, 'G': 2, 'T': 3}

The following function inserts a new sequence into the tree.

def insert(root, sequence):
    node = root
    for base in sequence:
        i = index_map[base]
        if node.children[i] is None:
            node.children[i] = Node()
        node = node.children[i]
    node.end = True

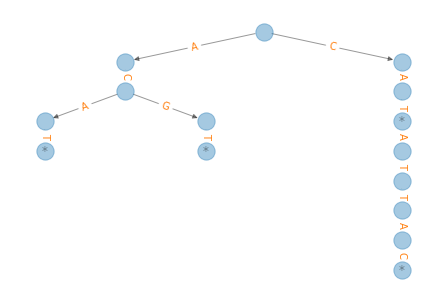
As an example, here’s a tree that contains only one sequence, CA.

node = Node()
insert(node, 'CA')
node

Node(False, [None, Node(False, [Node(True, [None, None, None, None]), None, None, None]), None, None])

The root of the tree has a single child, at index 1.

child = node.children[1]
child

Node(False, [Node(True, [None, None, None, None]), None, None, None])

The child has a single child, at index 0.

grandchild = child.children[0]
grandchild

Node(True, [None, None, None, None])

In the grandchild, end is True, which indicates that there is a sequence in the tree that ends at this node.

Here’s an example with more sequences.

tree = Node()
for sequence in ['ACGT', 'ACAT', 'CAT', 'CATATTAC']:
    insert(tree, sequence)

I’ll use NetworkX and EoN to draw this tree.

try:
    import EoN
except ImportError:
    !pip install EoN

import networkx as nx

def add_edges(parent, G):
    """Traverse the tree and add edges to G."""
    for child in parent.children:
        if child:
            G.add_edge(parent, child)
            add_edges(child, G)

G = nx.DiGraph()
add_edges(tree, G)

def get_labels(parent, labels):
    """Traverse the tree and add node labels to a dictionary."""
    if parent.end:
        labels[parent] = '*'
    else:
        labels[parent] = ''
        
    for child in parent.children:
        if child:
            get_labels(child, labels)

def get_edge_labels(parent, edge_labels):
    """Traverse the tree and add edge labels to a dictionary."""
    bases = 'ACGT'
    for i, child in enumerate(parent.children):
        if child:
            edge_labels[parent, child] = bases[i]
            get_edge_labels(child, edge_labels)

from EoN import hierarchy_pos

def draw_tree(tree):
    G = nx.DiGraph()
    add_edges(tree, G)
    pos = hierarchy_pos(G)
    labels = {}
    get_labels(tree, labels)
    edge_labels = {}
    get_edge_labels(tree, edge_labels)
    nx.draw(G, pos, labels=labels, alpha=0.4)
    nx.draw_networkx_edge_labels(G, pos, 
                                 edge_labels=edge_labels, 
                                 font_color='C1')

draw_tree(tree)

Question 1#

Write a function called find that takes as parameters

A Node that represents the root of a tree and
A string representing a sequence of bases.

It should return True if the sequence appears in the tree, and False otherwise.

You can use the following examples to test your code:

find(tree, 'CAT')  # should be True

True

find(tree, 'ACAT') # should be True

True

find(tree, 'TAG') # should be False

False

find(tree, 'CA') # should be False

False

Question 2#

Write a function called find_all_rec that takes as parameters:

A Node in a tree.
A path that indicates the sequence of bases from the root to the current Node.
A list of sequences.

This function should traverse the tree and add to the list all of the complete sequences it discovers.

Hint: Review make_table from huffman.ipynb.

You can use the following example to test your code.

t = []
find_all_rec(tree, '', t)
t

['ACAT', 'ACGT', 'CAT', 'CATATTAC']

The result should be a list with the following elements, not necessarily in this order

['ACAT', 'ACGT', 'CAT', 'CATATTAC']

Question 3#

Write a function called find_all that takes a Node and a sequence of bases. It should traverse the tree and return a list that contains all sequences in the tree that begin with the given prefix.

Note: You can use find_all_rec as part of your solution even if your answer to the previous question does not work.

You can use the following examples to test your code.

find_all(tree, 'CA')   # Should return ['CAT', 'CATATTAC']

['CAT', 'CATATTAC']

find_all(tree, 'A')    # Should return ['ACAT', 'ACGT']

['ACAT', 'ACGT']

find_all(tree, '')     # Should return all sequences in the tree

['ACAT', 'ACGT', 'CAT', 'CATATTAC']

Question 4#

Suppose we write a more general version of Node.__init__ that takes end and children as optional parameters.

class BadNode:
    def __init__(self, end=True, children=[None, None, None, None]):
        self.children = children
        self.end = end
        
    def __repr__(self):
        return f'Node({self.end}, {self.children})'

And we write a version of insert that uses BadNode:

def bad_insert(root, sequence):
    node = root
    for base in sequence:
        i = index_map[base]
        if node.children[i] is None:
            node.children[i] = BadNode(end=False)
        node = node.children[i]
    node.end = True

If we use the new versions to make a tree, like this:

tree2 = BadNode()
for sequence in ['ACGT', 'ACAT', 'CAT', 'CATATTAC']:
    bad_insert(tree2, sequence)

It seems to work. But if we draw the tree, we get a RecursionError.

draw_tree(tree2)

---------------------------------------------------------------------------
RecursionError                            Traceback (most recent call last)
<ipython-input-67-f08ae257619c> in <module>
----> 1 draw_tree(tree2)

<ipython-input-50-bd629f554f38> in draw_tree(tree)
      3 def draw_tree(tree):
      4     G = nx.DiGraph()
----> 5     add_edges(tree, G)
      6     pos = hierarchy_pos(G)
      7     labels = {}

<ipython-input-46-db255f1cfa96> in add_edges(parent, G)
      6         if child:
      7             G.add_edge(parent, child)
----> 8             add_edges(child, G)

... last 1 frames repeated, from the frame below ...

<ipython-input-46-db255f1cfa96> in add_edges(parent, G)
      6         if child:
      7             G.add_edge(parent, child)
----> 8             add_edges(child, G)

RecursionError: maximum recursion depth exceeded while calling a Python object

In the cell that defines BadNode, write a comment that explains what the problem is, and then fix it.

Note: Your fixed version should still accept end and children as optional parameters.

Data Structures and Information Retrieval in Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

Data Structures and Information Retrieval in Python

Quiz 6

Contents