Merge Sort#

Implementing Merge Sort#

Merge sort is a divide and conquer strategy:

Divide the sequence into two halves,
Sort the halves, and
Merge the sorted sub-sequences into a single sequence.

Since step 2 involves sorting, this algorithm is recursive, so we need a base case. There are two options:

If the size falls below some threshold, we can use another sort algorithm.
If the size of a sub-sequence is 1, it is already sorted.

To implement merge sort, I think it’s helpful to start with a non-recursive version that uses the Python sort function to sort the sub-sequences.

def merge_sort_norec(xs):
    n = len(xs)
    mid = n//2
    left = xs[:mid]
    right = xs[mid:]
    
    left.sort()
    right.sort()
    
    return merge(left, right)

Exercise: Write a function called merge that takes two sorted sequences, left and right, and returns a sequence that contains all elements from left and right, in ascending order (or non-decreasing order, to be more precise).

Note: this function is not conceptually difficult, but it is notoriously tricky to get all of the edge cases right without making the function unreadable. Take it as a challenge to write a version that is correct, concise, and readable. I found that I could write it more concisely as a generator function.

You can use the following example to test your code.

import random

population = range(100)
xs = random.sample(population, k=6)
ys = random.sample(population, k=6)
ys

[65, 55, 62, 4, 1, 91]

xs.sort()
ys.sort()
ys

[1, 4, 55, 62, 65, 91]

res = list(merge(xs, ys))
res

[1, 4, 13, 26, 55, 62, 65, 68, 71, 90, 91, 98]

sorted(res) == res

True

Exercise: Starting with merge_sort_norec, write a function called merge_sort_rec that’s fully recursive; that is, instead of using Python’s sort function to sort the halves, it should use merge_sort_rec. Of course, you will need a base case to avoid an infinite recursion.

Test your method by running the code in the next cell, then use test_merge_sort_rec, below, to check the performance of your function.

xs = random.sample(population, k=12)
xs

[5, 25, 67, 88, 35, 71, 26, 28, 12, 7, 57, 8]

res = list(merge_sort_rec(xs))
res

[5, 7, 8, 12, 25, 26, 28, 35, 57, 67, 71, 88]

sorted(res) == res

True

Heap Merge#

Suppose we want to merge more than two sub-sequences. A convenient way to do that is to use a heap. For example, here are three sorted sub-sequences.

xs = random.sample(population, k=5)
ys = random.sample(population, k=5)
zs = random.sample(population, k=5)

min(xs), min(ys), min(zs)

(3, 16, 12)

xs.sort()
ys.sort()
zs.sort()

For each sequence, I’ll make an iterator and push onto the heap a tuple that contains:

The first element from the iterator,
An index that’s different for each iterator, and
The iterator itself.

When the heap compares two of these tuples, it compares the elements first. If there’s a tie, it compares the indices. Since the indices are unique, there can’t be a tie, so we never have to compare iterators (which would be an error).

sequences = [xs, ys, zs]

from heapq import heappush, heappop

heap = []
for i, seq in enumerate(sequences):
    iterator = iter(seq)
    first = next(iterator)
    heappush(heap, (first, i, iterator))

When we pop a value from the heap, we get the tuple with the smallest value.

value, i, iterator = heappop(heap)
value

If we know that the iterator has more values, we can use next to get the next one and then push a tuple back into the heap.

heappush(heap, (next(iterator), i, iterator))

If we repeat this process, we’ll get all elements from all sub-sequences in ascending order.

However, we have to deal with the case where the iterator is empty. In Python, the only way to check is to call next and take your chances! If there are no more elements in the iterator, next raises a StopIteration exception, which you can handle with a try statement, like this:

iterator = iter(xs)

while True:
    try:
        print(next(iterator))
    except StopIteration:
        break

Exercise: Write a generator function called heapmerge that takes a list of sequences and yields the elements from the sequences in increasing order.

You can use the following examples to test your function.

seq = list(heapmerge([xs, ys, zs]))
seq

[3, 10, 12, 13, 16, 17, 20, 29, 34, 44, 87, 89, 92, 95, 97]

sorted(seq) == seq

True

The heapq module provides a function called merge that implements this algorithm.

Comparing sort algorithms#

NumPy provides implementations of three sorting algorithms, quicksort, mergesort, and heapsort.

In theory that are all in O(n log n). Let’s see what that looks like when we plot runtime versus problem size.

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve
        local, _ = urlretrieve(url, filename)
        print('Downloaded ' + local)
    
download('https://github.com/AllenDowney/DSIRP/raw/main/timing.py')

from timing import run_timing_test, plot_timing_test

import numpy as np

def test_quicksort(n):
    xs = np.random.normal(size=n)
    xs.sort(kind='quicksort')

ns, ts = run_timing_test(test_quicksort)
plot_timing_test(ns, ts, 'test_quicksort', exp=1)

1024 0.0
2048 0.0
4096 0.0
8192 0.0
16384 0.0
32768 0.0
65536 0.010000000000000231
131072 0.009999999999999787
262144 0.03000000000000025
524288 0.04999999999999982
1048576 0.1200000000000001
2097152 0.23999999999999977
4194304 0.5000000000000004
8388608 0.9699999999999993
16777216 2.0900000000000007

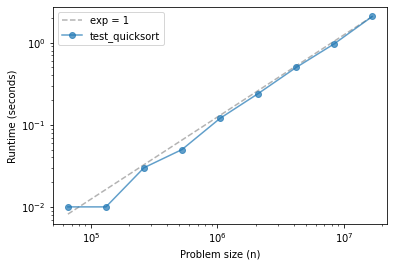
quicksort is hard to distinguish from linear, up to about 10 million elements.

def test_mergesort(n):
    xs = np.random.normal(size=n)
    xs.sort(kind='mergesort')

ns, ts = run_timing_test(test_mergesort)
plot_timing_test(ns, ts, 'test_mergesort', exp=1)

1024 0.0
2048 0.0
4096 0.0
8192 0.0
16384 0.0
32768 0.0
65536 0.010000000000000675
131072 0.009999999999999787
262144 0.03000000000000025
524288 0.05999999999999961
1048576 0.1200000000000001
2097152 0.2699999999999996
4194304 0.5499999999999998
8388608 1.160000000000001

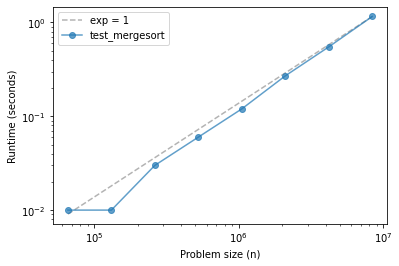
Merge sort is similar, maybe with some upward curvature.

def test_heapsort(n):
    xs = np.random.normal(size=n)
    xs.sort(kind='heapsort')

ns, ts = run_timing_test(test_quicksort)
plot_timing_test(ns, ts, 'test_heapsort', exp=1)

1024 0.0
2048 0.0
4096 0.0
8192 0.0
16384 0.0
32768 0.0
65536 0.009999999999999787
131072 0.009999999999999787
262144 0.030000000000001137
524288 0.049999999999998934
1048576 0.10999999999999943
2097152 0.21000000000000085
4194304 0.4499999999999993
8388608 0.9800000000000004
16777216 1.9700000000000006

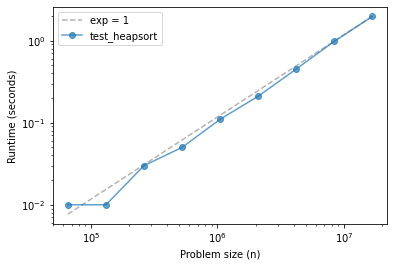
The three methods are effectively linear over this range of problem sizes.

And their run times are about the same, with quicksort being the fastest, despite being the one with the worst asympotic performance in the worst case.

Now let’s see how our implementation of merge sort does.

def test_merge_sort_rec(n):
    xs = np.random.normal(size=n)
    spectrum = merge_sort_rec(xs)

ns, ts = run_timing_test(test_merge_sort_rec)
plot_timing_test(ns, ts, 'test_merge_sort_rec', exp=1)

0.0
0.009999999999999787
0.010000000000001563
0.02999999999999936
0.0600000000000005
0.11999999999999922
0.2599999999999998
131072 0.5300000000000011
262144 1.089999999999998

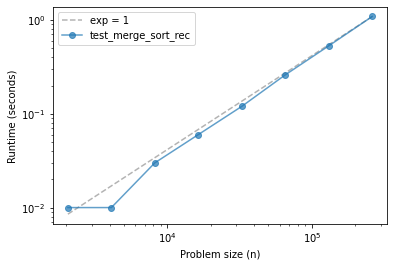
If things go according to plan, our implementation of merge sort should be close to linear, or a little steeper.

Data Structures and Information Retrieval in Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

Data Structures and Information Retrieval in Python

Merge Sort

Contents

Merge Sort#

Implementing Merge Sort#

Heap Merge#

Comparing sort algorithms#