Deque#

Double-ended Queue#

With Python lists, we can add and remove elements from the end of the list in constant time, but adding and removing from the beginning takes linear time. That’s because Python lists are implemented using arrays that grow dynamically.

With linked lists, we can add and remove elements from the beginning of the list in constant time, but adding and removing from the end takes linear time.

With either of these implementations, it is easy to make a stack, that is, a collection where the first element we add is the last element we remove. A stack is also called a “first-in, last-out” queue, abbreviated FILO.

But it is not easy to implement a “first-in, first-out” queue, that is, a collection where the first element we add is the first element we remove.

Fortunately, there are ways to implement lists that can add and remove elements from both ends in constant time. A collection that has this property is called a double-ended queue, abbreviated “deque” and pronounced like “deck”.

One way to implement a deque is a doubly-linked list, also known as a “head-tail linked list”. Each node in a doubly-linked list has a reference to the previous node in the list as well as the next element, which I will call left and right.

class Node:
    def __init__(self, data, left=None, right=None):
        self.data = data
        self.left = left
        self.right = right
        
    def __repr__(self):
        return f'Node({self.data})'

We can create nodes like this:

node1 = Node(1)
node2 = Node(2)
node3 = Node(3)

node1

Node(1)

And then link them up, like this:

node1.right = node2
node2.right = node3

node2.left = node1
node3.left = node2

To traverse the list from left to right, we can start at the beginning and follow the right links.

node = node1
while node:
    print(node)
    node = node.right

Node(1)
Node(2)
Node(3)

To traverse from right to left, we start and the end and follow the left links.

node = node3
while node:
    print(node)
    node = node.left

Node(3)
Node(2)
Node(1)

Deque objects#

For some operations, it will be convenient to have another object that represents the whole list (as opposed to one of its nodes).

Here’s the class definition.

class Deque:
    def __init__(self, head=None, tail=None):
        self.head = head
        self.tail = tail
        
    def __repr__(self):
        return f'LinkedList({self.head}, {self.tail})'

Now we can create a Deque with references to node1 and node3:

deque = Deque(node1, node3)
deque

LinkedList(Node(1), Node(3))

For debugging purposes, I’ll use the following function, which prints the list from right to left and then left to right, which confirms that all of the links are correct.

def print_deque(deque):
    node = deque.head
    while node:
        print(node.data, end=', ')
        node = node.right
    print()
    
    node = deque.tail
    while node:
        print(node.data, end=', ')
        node = node.left
    print()

Here’s an example.

print_deque(deque)

1, 2, 3, 
3, 2, 1, 

Push#

Now let’s see how we can add and remove elements from the beginning and end in constant time. We’ll start with the push operations.

If we start with an empty deque, adding the first node is a special case, so I’ll pull that into a function.

def push_first(deque, value):
    deque.head = deque.tail = Node(value, None, None)

Here’s an example.

deque = Deque()
push_first(deque, 1)
print_deque(deque)

1, 
1, 

Exercise: Write left_push, which takes a Deque object and a new value, and adds the value to the beginning of the deque.

If the queue is empty, it should call push_first to handle the special case; otherwise it should handle the general case.

You can use the following examples to test your function:

deque = Deque()
left_push(deque, 2)
print_deque(deque)

2, 
2, 

left_push(deque, 1)
print_deque(deque)

1, 2, 
2, 1, 

Exercise: Write right_push, which takes a Deque object and a new value, and adds the value to the end of the deque.

If the queue is empty, it should call push_first to handle the special case; otherwise it should handle the general case.

You can use the following examples to test your function:

deque = Deque()
right_push(deque, 3)
print_deque(deque)

3, 
3, 

right_push(deque, 4)
print_deque(deque)

3, 4, 
4, 3, 

Pop#

To pop elements from the deque, we have to handle two special cases:

If head and tail are both None, the deque is empty and we should raise a ValueError.
If head and tail refer to the same Node, there is only one element, so we should remove it and leave the deque empty.

The following function handles these cases.

def pop_last(deque):
    if deque.head is None:
        raise ValueError('Tried to pop from empty deque')
    
    old_head = deque.head
    deque.head = deque.tail = None
    return old_head.data

We can test it like this:

deque = Deque()
left_push(deque, 1)
pop_last(deque)

print_deque(deque)

Exercise: Write left_pop, which takes a Deque object, remove the first node, and return the first data value.

If the queue is empty or has a single element, it should call pop_last to handle the special case; otherwise it should handle the general case.

You can use the following example to test your code.

deque = Deque()
left_push(deque, 2)
left_push(deque, 1)
print_deque(deque)

1, 2, 
2, 1, 

left_pop(deque)

Check to see whether the remaining list is well-formed.

print_deque(deque)

2, 
2, 

left_pop(deque)

try:
    left_pop(deque)
except ValueError as e:
    print(e)

Tried to pop from empty deque

Exercise: Write right_pop, which takes a Deque object, remove the last node, and return the last data value.

If the queue is empty or has a single element, it should call pop_last to handle the special case; otherwise it should handle the general case.

You can use the following examples to test your function.

deque = Deque()
left_push(deque, 2)
left_push(deque, 1)
print(deque)

LinkedList(Node(1), Node(2))

right_pop(deque)

print_deque(deque)

1, 
1, 

right_pop(deque)

try:
    right_pop(deque)
except ValueError as e:
    print(e)

Tried to pop from empty deque

collections.deque#

The Python collections module provides an implementation of a deque. You can read the documentation here and the source code here.

To confirm that it can add and remove elements from the beginning and end in constant time, let’s run some timing tests.

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve
        local, _ = urlretrieve(url, filename)
        print('Downloaded ' + local)
    
download('https://github.com/AllenDowney/DSIRP/raw/main/timing.py')

from collections import deque

def appendleft(n):
    d = deque()
    [d.appendleft(x) for x in range(n)]

def popleft(n):
    d = deque()
    [d.appendleft(x) for x in range(n)]    
    [d.popleft() for _ in range(n)]

from timing import run_timing_test

ns, ts = run_timing_test(appendleft)

1024 0.0
2048 0.0
4096 0.0
8192 0.0
16384 0.0
32768 0.0
65536 0.009999999999999787
131072 0.0
262144 0.010000000000000231
524288 0.029999999999999805
1048576 0.06999999999999984
2097152 0.1200000000000001
4194304 0.25
8388608 0.5100000000000002
16777216 1.0299999999999998

def append(n):
    d = deque()
    [d.append(x) for x in range(n)]

from timing import plot_timing_test

plot_timing_test(ns, ts, scale='linear')

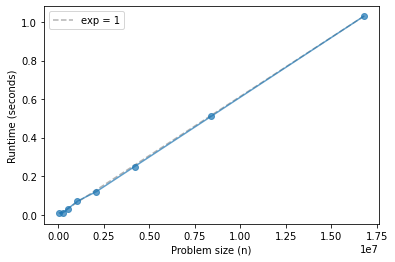
Running these operations n times is linear in n, which means that each one is constant time, at least on average.

Exercise: Modify the examples above to confirm that append and pop are also constant time.

Data Structures and Information Retrieval in Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

Data Structures and Information Retrieval in Python

Deque

Contents