Priority Queues and Heaps#

The `heapq` module#

The heapq module provides functions for adding and removing elements to and from a heap.

from heapq import heappush, heappop

The heap itself is literally a list, so if you create an empty list, you can think of it as a heap with no elements.

heap = []

Then you can use heappush to add one element at a time.

data = [4, 9, 3, 7, 5, 1, 6, 8, 2]

for x in data:
    heappush(heap, x)
    
heap

[1, 2, 3, 5, 7, 4, 6, 9, 8]

The result is a list that represents a tree. Here’s how the correspondence works between the list representation and the tree representation:

The first element (index 0) is the root.
The next two elements are the children of the root.
The next four element are the grandchildren of the root.

And so on.

In general, if the index of an element is i, its parent is (i-1)//2 and its children are 2*i + 1 and 2*i + 2.

Drawing the Tree#

To generate the tree representation of the heap, the following function iterates through the heap and makes a NetworkX graph with an edge between each node and its parent.

import networkx as nx

def make_dag(heap):
    """Make a NetworkX graph that represents the heap."""
    G = nx.DiGraph()
    
    for i in range(1, len(heap)):
        parent = (i-1)//2
        G.add_edge(parent, i)
    
    return G

G = make_dag(heap)

To draw the tree, we’ll use a module called EoN that provides a function called hierarchy_pos.

It takes as a parameter a NetworkX graph that represents a tree, and it returns a dictionary that maps from each node to a position in the Cartesian plane. If we pass this dictionary to nx.draw, it lays the tree out accordingly.

try:
    import EoN
except ImportError:
    !pip install EoN

Collecting EoN
  Using cached EoN-1.1-py3-none-any.whl
Requirement already satisfied: numpy in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from EoN) (1.21.4)
Requirement already satisfied: scipy in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from EoN) (1.7.3)
Requirement already satisfied: matplotlib in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from EoN) (3.5.1)
Requirement already satisfied: networkx in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from EoN) (2.6.3)
Requirement already satisfied: cycler>=0.10 in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from matplotlib->EoN) (0.11.0)
Requirement already satisfied: python-dateutil>=2.7 in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from matplotlib->EoN) (2.8.2)
Requirement already satisfied: pyparsing>=2.2.1 in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from matplotlib->EoN) (3.0.6)
Requirement already satisfied: fonttools>=4.22.0 in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from matplotlib->EoN) (4.28.5)
Requirement already satisfied: packaging>=20.0 in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from matplotlib->EoN) (21.3)
Requirement already satisfied: pillow>=6.2.0 in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from matplotlib->EoN) (8.4.0)
Requirement already satisfied: kiwisolver>=1.0.1 in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from matplotlib->EoN) (1.3.2)
Requirement already satisfied: six>=1.5 in /home/downey/anaconda3/envs/DSIRP/lib/python3.10/site-packages (from python-dateutil>=2.7->matplotlib->EoN) (1.16.0)
Installing collected packages: EoN
Successfully installed EoN-1.1

from EoN import hierarchy_pos

def draw_heap(heap):
    G = make_dag(heap)
    pos = hierarchy_pos(G)
    labels = dict(enumerate(heap))
    nx.draw(G, pos, labels=labels, alpha=0.4)

Here’s what the tree representation looks like.

print(heap)
draw_heap(heap)

[1, 2, 3, 5, 7, 4, 6, 9, 8]

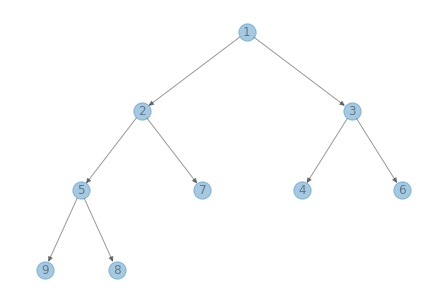
The Heap Property#

If the list is a heap, the tree should have the heap property:

Every parent is less than or equal to its children.

Or more formally:

For all pairs of nodes P and C, where P is the parent of C, the value of P must be less than or equal to the value of C.

The following function checks whether this property is true for all nodes.

def is_heap(heap):
    """Check if a sequence has the heap property.
    
    Every child should be >= its parent.
    """
    for i in range(1, len(heap)):
        parent = (i-1) // 2
        if heap[parent] > heap[i]:
            return False
    return True

As we might hope, heap is a heap.

is_heap(heap)

True

Here’s a list of integers in no particular order, and as you might expect, it does not have the heap property.

data = [4, 9, 3, 7, 5, 1, 6, 8, 2]
is_heap(data)

False

Using a Heap to Sort#

Given a heap, we can implement a sort algorithm called heapsort.

Let’s start again with a fresh heap:

heap = []
for x in data:
    heappush(heap, x)

If we know that a list is a heap, we can use heappop to find and remove the smallest element.

heappop(heap)

heappop rearranges the remaining elements of the list to restore the heap property (we’ll see how soon).

heap

[2, 5, 3, 8, 7, 4, 6, 9]

is_heap(heap)

True

And that means we can use heappop again to get the second smallest element (of the original heap):

heappop(heap)

Which means we can use a heap to sort a list.

Exercise: Write a generator function called heapsort that takes an iterable and yields the elements of the iterable in increasing order.

Now let’s see how a heap is implemented. The two key methods are push and pop.

Push#

To insert an element in a heap, you start by appending it to the list.

The result is generally not a heap, so you have to do some work to restore the heap property:

If the new element is greater than or equal to its parent, you are done.
Otherwise swap the new element with its parent.
If the new element is greater than or equal to the parent’s parent, you are done.
Otherwise swap the new element with its parent’s parent.
And repeat, working your way up the tree, until you’re done or you reach the root.

This process is called “sift-up” or sometimes swim.

Exercise: Write a function called push that does the same thing as heappush: it should take as parameters a list (which should be a heap) and a new element; it should add the new element to the list and restore the heap property.

You can use this example to test your code:

heap = []
for x in data:
    push(heap, x)
    assert is_heap(heap)

heap

[1, 2, 3, 5, 7, 4, 6, 9, 8]

is_heap(heap)

True

Pop#

To remove an element from the heap, you:

Make a copy of the root element,
Pop the last element off the list and store it at the root.
Then you have to restore the heap property. If the new root is less than or equal to both of its children, you are done.
Otherwise, swap the parent with the smaller of its children.
Then repeat the process with the child you just replaced, and continue until you get to a leaf node.

This process is called a “sift-down” or sometimes “sink”.

Exercise: Write a function called pop that does the same thing as heappop: it should remove the smallest element, restore the heap property, and return the smallest element.

Hint: This one is tricky because you have to deal with several special cases.

heap = []
for x in data:
    heappush(heap, x)

while heap:
    print(pop(heap))
    assert is_heap(heap)

Data Structures and Information Retrieval in Python

License: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International

Data Structures and Information Retrieval in Python

Priority Queues and Heaps

Contents