10. Penguins, Pessimists, and Paradoxes

Probably Overthinking It is available from Bookshop.org and Amazon (affiliate links).

If you like Probably Overthinking It, you’ll like my book in progress, You Would Choose Now, which uses decades of survey data to track changing attitudes in the United States. The early access edition is available now.

Click here to run this notebook on Colab.

Show code cell content

Hide code cell content

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

from utils import set_pyplot_params, decorate

set_pyplot_params()

# Set the random seed so we get the same results every time
np.random.seed(17)

In 2021, the journalist I mentioned in the previous chapter wrote a series of misleading articles about the COVID pandemic. I won’t name him, but on April 1, appropriately, The Atlantic magazine identified him as “The Pandemic’s Wrongest Man”.

In November, this journalist posted an online newsletter with the title “Vaccinated English adults under 60 are dying at twice the rate of unvaccinated people the same age”. It includes a graph showing that the overall death rate among young, vaccinated people increased between April and September, 2021, and was actually higher among the vaccinated than among the unvaccinated.

As you might expect, this newsletter got a lot of attention. Among skeptics, it seemed like proof that vaccines were not just ineffective, but harmful. And among people who were counting on vaccines to end the pandemic, it seemed like a devastating setback.

Many people fact-checked the article, and at first the results held up to scrutiny: the graph accurately represented data published by the U.K. Office for National Statistics. Specifically, it showed death rates, from any cause, for people in England between 10 and 59 years old, from March to September 2021. And between April and September, these rates were higher among the fully vaccinated, compared to the unvaccinated, by a factor of almost 2. So the journalist’s description of the results was correct.

However, his conclusion that vaccines were causing increased mortality was completely wrong. In fact, the data he reported shows that vaccines were safe and effective in this population, and demonstrably saved many lives.

How, you might ask, can increased mortality be evidence of saved lives? The answer is Simpson’s paradox. If you have not seen it before, Simpson’s paradox can seem impossible, but as I will try to show you, it is not just possible but ordinary – and once you’ve seen enough examples, it is not even surprising.

We’ll start with an easy case and work our way up.

10.1. Old Optimists, Young Pessimists

Would you say that most of the time people try to be helpful, or that they are mostly just looking out for themselves? Almost every year since 1972, the General Social Survey (GSS) has posed that question to a representative sample of adult residents of the United States.

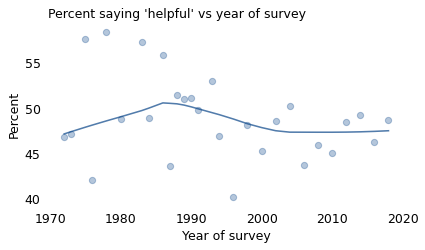
The following figure shows how the responses have changed over time. The circles show the percentage of people in each survey who said that people try to be helpful.

Show code cell content

Hide code cell content

# https://gssdataexplorer.norc.org/variables/439/vshow

# 1 = helpful
# 2 = look out for themselves
# 3 = depends

Show code cell content

Hide code cell content

gss = pd.read_hdf(filename, "gss")
gss.shape

(68846, 214)

Show code cell content

Hide code cell content

year = gss["year"] == 1978
series = gss.loc[year, "helpful"]
series.describe()

count    1520.000000
mean        1.474342
std         0.605548
min         1.000000
25%         1.000000
50%         1.000000
75%         2.000000
max         3.000000
Name: helpful, dtype: float64

Show code cell content

Hide code cell content

series.value_counts()

helpful
1.0    888
2.0    543
3.0     89
Name: count, dtype: int64

Show code cell source

Hide code cell source

from empiricaldist import Pmf

Pmf.from_seq(series)

	probs
helpful
1.0	0.584211
2.0	0.357237
3.0	0.058553

Show code cell content

Hide code cell content

year = gss["year"] == 1987
series = gss.loc[year, "helpful"]
series.describe()

count    1809.000000
mean        1.606965
std         0.571034
min         1.000000
25%         1.000000
50%         2.000000
75%         2.000000
max         3.000000
Name: helpful, dtype: float64

Show code cell content

Hide code cell content

series.value_counts()

helpful
2.0    940
1.0    790
3.0     79
Name: count, dtype: int64

Show code cell source

Hide code cell source

from empiricaldist import Pmf

Pmf.from_seq(series)

	probs
helpful
1.0	0.436705
2.0	0.519624
3.0	0.043671

Show code cell content

Hide code cell content

xtab = pd.crosstab(gss["year"], gss["helpful"], normalize="index")
series = xtab[1] * 100
series.name = "helpful"
series.max(), series.idxmax(), series.min(), series.idxmin()

(58.42105263157895, 1978, 40.243902439024396, 1996)

Show code cell content

Hide code cell content

title = """Would you say that most of the time people try to be helpful, 
or that they are mostly just looking out for themselves?
"""

short_title = "Would people be helpful or look out for themselves?"

Show code cell source

Hide code cell source

from utils import plot_series_lowess

plot_series_lowess(series, plot_series=True, color="C0", label="")

# plt.title(title, loc="left", fontdict=dict(fontsize=12))
decorate(
    xlabel="Year of survey",
    ylabel="Percent",
    title="Percent saying 'helpful' vs year of survey",
)

Show code cell content

Hide code cell content

from utils import make_lowess

make_lowess(series)

1972.0    46.399992
1973.0    46.804000
1975.0    47.621057
1976.0    48.027929
1978.0    48.815860
1980.0    49.546170
1983.0    50.731526
1984.0    51.032275
1986.0    51.262427
1987.0    51.154733
1988.0    51.145142
1989.0    50.812748
1990.0    50.518220
1991.0    50.078283
1993.0    49.243129
1994.0    48.868180
1996.0    48.351256
1998.0    48.030031
2000.0    47.515587
2002.0    47.034961
2004.0    46.911821
2006.0    46.962785
2008.0    47.104853
2010.0    47.228283
2012.0    47.357632
2014.0    47.510421
2016.0    47.688959
2018.0    47.887754
dtype: float64

The percentages vary from year to year, in part because the GSS surveys a different group of people for each survey. Looking at the extremes: in 1978, about 58% said “helpful”; in 1996, it was only 40%.

The solid line in the figure shows a LOWESS curve, which is a statistical way to smooth out short-term variation and show the long-term trend. Putting aside the extreme highs and lows, it looks like the fraction of optimists has decreased since 1990, from about 51% to 48%.

These results don’t just depend on when you ask; they also depend on who you ask. In particular, they depend strongly on when the respondents were born, as shown in the following figure.

Show code cell source

Hide code cell source

from utils import prepare_yvar
from utils import chunk_series

xvarname = "cohort"
yvarname = "helpful"
yvalue = 1

prepare_yvar(gss, yvarname, yvalue)
series = chunk_series(gss, xvarname, size=600) * 100
plot_series_lowess(
    series,
    plot_series=True,
    color="C1",
    ls="dashed",
    label="",
)

# plt.title(title, loc="left", fontdict=dict(fontsize=11))
decorate(
    xlabel="Year of birth",
    ylabel="Percent",
    title="Percent saying 'helpful' vs year of birth",
)

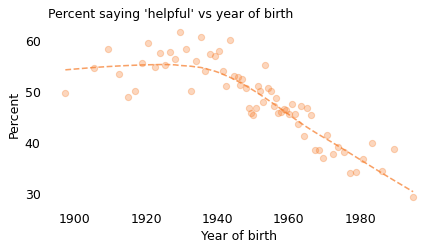
Notice that the x-axis here is the respondent’s year of birth, not the year they participated in the survey. The oldest person to participate in the GSS was born in 1883. Because the GSS only surveys adults, the youngest, as of 2021, was born in 2003. Again, the markers show variability in the survey results; the dashed line shows the long-term trend.

Starting with people born in the 1940s, Americans’ faith in humanity has been declining consistently, from about 55% for people born before 1930 to about 30% for people born after 1990. That is a substantial decrease!

Show code cell content

Hide code cell content

make_lowess(series)

1897.305000    52.120319
1905.215000    53.284864
1909.190000    53.858843
1912.293333    54.306193
1914.818333    54.665509
                 ...    
1980.853333    36.307102
1983.280000    35.352350
1986.106667    34.266167
1989.426667    33.030785
1994.888325    31.071020
Length: 68, dtype: float64

To get an idea of what’s happening, let’s zoom in on people born in the 1940s. The following figure shows the fraction of people in this cohort who said people would try to be helpful, plotted over time.

Show code cell content

Hide code cell content

subset = gss.dropna(subset=["cohort10"]).copy()
subset["cohort10"] = subset["cohort10"].astype(int)

Show code cell content

Hide code cell content

from utils import make_table

xvarname = "year"
yvarname = "helpful"
gvarname = "cohort10"
yvalue = 1

prepare_yvar(gss, yvarname, yvalue)
overall = chunk_series(subset, xvarname) * 100
table = make_table(subset, xvarname, yvarname, gvarname, yvalue)
del table[1900]
del table[1910]
series = table[1940]

Show code cell content

Hide code cell content

make_lowess(series)

1972.000000    45.969222
1972.853333    46.838756
1974.640000    48.553441
1975.906667    49.690533
1977.753333    51.209736
1979.553333    52.588674
1982.690000    52.934442
1983.920000    52.947150
1986.003333    52.592398
1987.000000    52.654427
1988.333333    53.031651
1989.936667    53.287806
1992.193333    53.422913
1993.943333    53.406083
1995.486667    53.295321
1997.220000    52.995021
1999.373333    53.017955
2001.793333    53.620756
2005.806667    55.357242
2009.146667    56.867664
2013.180000    58.812900
2016.970370    60.725940
dtype: float64

Show code cell source

Hide code cell source

plot_series_lowess(series, plot_series=True, color="C2", label="Born in the 1940s")

decorate(
    xlabel="Year of survey",
    ylabel="Percent",
    title="Percent saying 'helpful' vs year of survey",
    loc="lower right",
)

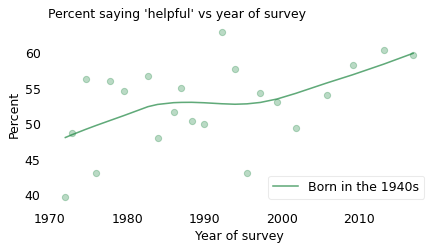
Again, different people were surveyed each year, so there is a lot of variability. Nevertheless, there is a clear increasing trend. When this cohort was interviewed in the 1970s, about 46% of them gave a positive response; when they were interviewed in the 2010s, about 61% did.

So that’s surprising. So far, we’ve seen that

• People have become more pessimistic over time,

• And successive generations have become more pessimistic,

• But if we follow one cohort over time, they become more optimistic as they age.

Now, maybe there’s something unusual about people born in the 1940s. They were children during the aftermath of World War II and they were young adults during the rise of the Soviet Union and the Cold War. These experiences might have made them more distrustful when they were interviewed in the 1970s. Then, from the 1980s to the present, they enjoyed decades of relative peace and increasing prosperity. And when they were interviewed in the 2010s, most were retired and many were wealthy. So maybe that put them in a more positive frame of mind.

However, there is a problem with this line of conjecture: it wasn’t just one cohort that trended toward the positive over time. It was all of them.

The following figure shows the responses to this question grouped by decade of birth and plotted over time. For clarity, I’ve dropped the circles showing the annual results and plotted only the smoothed lines.

Show code cell source

Hide code cell source

from utils import visualize_table, label_table

visualize_table(
    overall,
    table,
    xlabel="Year of survey",
    ylabel="Percent",
    title="Percent saying 'helpful' vs year of survey",
    plot_series=False,
)
nudge = {"1900s": 1, "1910s": 1, "1920s": 2}
label_table(table, nudge)

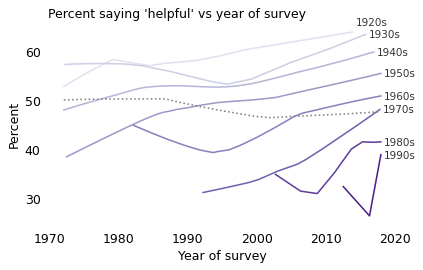
The solid lines show the trends within each cohort: people generally become more optimistic as they age. The dashed line shows the overall trend: on average, people are becoming less optimistic over time.

This is an example of Simpson’s paradox, named for Edward H. Simpson, a codebreaker who worked at Bletchley Park during World War II. For people who have not seen it before, the effect often seems impossible: if all of the groups are increasing, and we combine them into a single group, how can the aggregate decrease?

In this example, the explanation is generational replacement; as the oldest, more optimistic cohort dies off, it is replaced by the youngest, more pessimistic cohort.

The differences between these generations are substantial. In the most recent data, only 39% of respondents born in the 1990s said people would try to be helpful, compared to 51% of those born in the 1960s and 64% of those born in the 1920s.

Show code cell content

Hide code cell content

table[1920].iloc[-1]

64.21052631578948

Show code cell content

Hide code cell content

table[1960].iloc[-1]

50.847457627118644

Show code cell content

Hide code cell content

table[1990].iloc[-1]

38.864628820960704

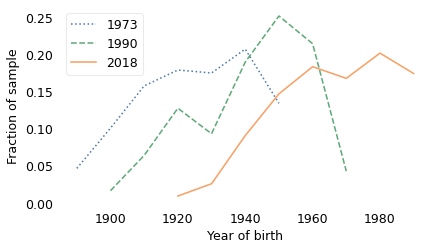
And the composition of the population has changed a lot over 50 years. The following figure shows the distribution of birth years for the respondents at the beginning of the survey in 1973, near the middle in 1990, and most recently in 2018.

Show code cell source

Hide code cell source

xtab = pd.crosstab(gss["year"], gss["cohort10"], normalize="index").replace(0, np.nan)

Pmf(xtab.loc[1973]).plot(ls=":", label="1973")
Pmf(xtab.loc[1990]).plot(color="C2", ls="--", label="1990")
Pmf(xtab.loc[2018]).plot(color="C1", label="2018")

decorate(xlabel="Year of birth", ylabel="Fraction of sample")

Show code cell source

Hide code cell source

from seaborn import kdeplot

options = dict(bw_adjust=2, cut=0, alpha=0.6)

kdeplot(gss.query("year==1973")["cohort"], ls=":", label="1973", **options)
kdeplot(gss.query("year==1990")["cohort"], color="C2", ls="--", label="1990", **options)
kdeplot(gss.query("year==2018")["cohort"], color="C1", label="2018", **options)

decorate(
    xlabel="Year of birth",
    ylabel="Relative likelihood",
    yticks=[],
    title="Distribution of birth year",
)

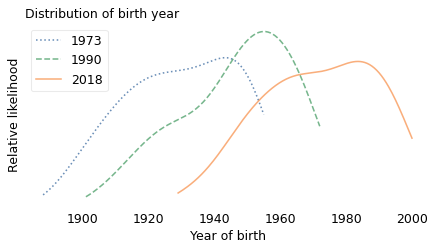
In the earliest years of the survey, most of the respondents were born between 1890 and 1950. In the 1990 survey, most were born between 1901 and 1972. In the 2018 survey, most were born between 1929 and 2000.

Show code cell content

Hide code cell content

series = gss.query("year==1973")["cohort"]
series.min(), series.max()

(1888.0, 1955.0)

Show code cell content

Hide code cell content

series = gss.query("year==1990")["cohort"]
series.min(), series.max()

(1901.0, 1972.0)

Show code cell content

Hide code cell content

series = gss.query("year==2018")["cohort"]
series.min(), series.max()

(1929.0, 2000.0)

With this explanation, I hope Simpson’s paradox no longer seems impossible. But if it is still surprising, let’s look at another example.

10.2. Real Wages

In April 2013 Floyd Norris, chief financial correspondent of The New York Times, wrote an article with the headline “Median Pay in U.S. Is Stagnant, but Low-Paid Workers Lose”. Using data from the U.S. Bureau of Labor Statistics, he computed the following changes in median real wages between 2000 and 2013, grouped by level of education:

• High School Dropouts: -7.9%

• High School Graduates, No College: -4.7%

• Some College: -7.6%

• Bachelor’s or Higher: -1.2%

In all groups, real wages were lower in 2013 than in 2000, which is what the article was about. But Norris also reported the overall change in the median real wage: during the same period, it increased by 0.9%. Several readers wrote to say he had made a mistake. If wages in all groups were doing down, how could overall wages go up?

To explain what’s going on, I will replicate the results from Norris’s article using data from the Current Population Survey (CPS) conducted by the U.S. Census Bureau and the Bureau of Labor Statistics. This dataset includes real wages and education levels for almost 1.9 million participants between 1996 and 2021. Real wages are adjusted for inflation and reported in constant 1999 dollars.

Show code cell source

Hide code cell source

ipums_cps = pd.read_hdf(filename, "ipums_cps")
ipums_cps.head()

	year	degree	real_wage
4	1970	hs	19068.0
7	1970	nohs	0.0
10	1970	hs	0.0
13	1970	nohs	0.0
17	1970	nohs	908.0

Show code cell content

Hide code cell content

d = {
    "nohs": "No diploma",
    "hs": "High school",
    "bach": "Bachelor",
    "assc": "Associate",
    "college": "Some college",
    "adv": "Advanced",
}
ipums_cps = ipums_cps.replace({"degree": d})

Show code cell source

Hide code cell source

start = 1996
recent = ipums_cps[ipums_cps["year"] >= start]
recent.head()

	year	degree	real_wage
3990996	1996	No diploma	67766.0
3991000	1996	Some college	3060.4
3991003	1996	No diploma	0.0
3991004	1996	Advanced	17488.0
3991008	1996	Bachelor	14209.0

Show code cell content

Hide code cell content

recent["real_wage"].describe()

count    1.896422e+06
mean     2.043957e+04
std      3.659772e+04
min      0.000000e+00
25%      0.000000e+00
50%      9.022000e+03
75%      2.963200e+04
max      1.303999e+06
Name: real_wage, dtype: float64

Show code cell content

Hide code cell content

recent["degree"].describe()

count         1896422
unique              6
top       High school
freq           582123
Name: degree, dtype: object

Show code cell content

Hide code cell content

recent["year"].describe()

count    1.896422e+06
mean     2.008845e+03
std      7.023367e+00
min      1.996000e+03
25%      2.003000e+03
50%      2.009000e+03
75%      2.015000e+03
max      2.021000e+03
Name: year, dtype: float64

Show code cell content

Hide code cell content

xvarname = "year"
yvarname = "real_wage"
gvarname = "degree"

Show code cell content

Hide code cell content

overall = recent.groupby("year")["real_wage"].mean()
overall.name = "overall"

Show code cell content

Hide code cell content

from scipy.stats import linregress

res = linregress(overall.index, overall)
res.slope

77.26163851752604

Show code cell content

Hide code cell content

table = pd.pivot_table(
    recent, index="year", columns="degree", values="real_wage", aggfunc="mean"
)

Show code cell content

Hide code cell content

for name, column in table.items():
    res = linregress(column.index, column)
    print(name, res.slope)

Advanced -150.74230565418188
Associate -188.32190788749065
Bachelor -53.36321685585188
High school -89.6395950955906
No diploma -26.70858108935015
Some college -148.96847910461423

Show code cell content

Hide code cell content

columns = [
    "Advanced",
    "Bachelor",
    "Associate",
    "Some college",
    "High school",
    "No diploma",
]

The following figure shows average real wages for each level of education over time.

Show code cell source

Hide code cell source

# figwidth = 3.835
# plt.figure(figsize=(figwidth, 0.6 * figwidth))

nudge = {"High school": -1.7}

table2 = table / 1000
for column in table2.columns:
    series = table2[column]
    series.plot(label="", alpha=0.6)
    x = series.index[-1] + 0.5
    y = series.values[-1] + nudge.get(column, 0) - 1
    plt.text(x, y, column)

overall2 = overall / 1000
overall2.plot(ls=":", color="gray", label="")

decorate(
    xlabel="Year",
    ylabel="1999 dollars (thousands)",
    title="Average real wage income by education level",
    xlim=[1996, 2022],
)
plt.xticks([2000, 2010, 2020])
plt.yticks([10, 30, 50])

([<matplotlib.axis.YTick at 0x7538660f4c70>,
  <matplotlib.axis.YTick at 0x753865f36680>,
  <matplotlib.axis.YTick at 0x753865f37730>],
 [Text(0, 10, '10'), Text(0, 30, '30'), Text(0, 50, '50')])

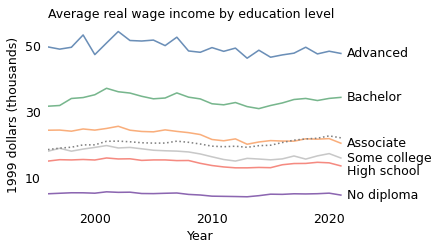
These results are consistent with Norris’s: real wages in every group decreased over this period. The decrease was steepest among people with an associate degree, by about $190 per year over 26 years.

The decrease was smallest among people with no high school diploma, about $30 per year.

However, if we combine the groups, real wages increased during the same period by about $80 per year, as shown by the dotted line in the figure. Again, this seems like a contradiction.

In this example, the explanation is that levels of education changed substantially during this period. The following figure shows the fraction of the population at each educational level, plotted over time.

Show code cell source

Hide code cell source

xtab = pd.crosstab(recent["year"], recent["degree"], normalize="index") * 100
xtab

degree	Advanced	Associate	Bachelor	High school	No diploma	Some college
year
1996	6.407083	6.425194	13.955126	32.711540	22.181306	18.319750
1997	6.413669	6.337339	14.177790	33.135006	21.450660	18.485536
1998	6.561266	6.693503	14.246543	33.138868	21.130622	18.229197
1999	6.731085	6.553290	14.739588	32.882404	20.543048	18.550585
2000	7.237661	6.802157	15.022058	32.606237	19.940802	18.391086
2001	7.242623	7.279962	15.264699	32.047467	19.786234	18.379015
2002	7.554037	7.265446	15.546263	31.826374	19.745568	18.062312
2003	7.619399	7.385120	15.668110	31.453953	19.497431	18.375987
2004	8.010435	7.387682	15.799661	31.305979	19.099773	18.396470
2005	7.982642	7.603384	15.930032	31.509980	18.947074	18.026888
2006	8.034985	7.982532	15.817465	31.691043	18.469364	18.004611
2007	8.141195	7.759157	16.636356	31.313698	18.050995	18.098598
2008	8.681550	7.725637	17.020391	30.919684	17.194194	18.458544
2009	8.832957	8.086253	16.873073	30.600277	17.113475	18.493966
2010	8.734951	8.249743	16.902414	30.866961	16.782624	18.463307
2011	9.223517	8.532432	17.356106	30.139945	16.330585	18.417415
2012	9.224073	8.566742	17.470351	30.036588	15.963916	18.738330
2013	9.542894	8.829571	17.472620	29.659596	15.559504	18.935814
2014	9.884352	8.814772	18.153473	29.687560	15.184972	18.274871
2015	10.178812	8.615827	18.279681	29.828693	14.816013	18.280975
2016	10.609366	9.099067	18.717212	29.282401	14.255343	18.036612
2017	10.867206	9.224281	19.028257	29.072627	13.952498	17.855131
2018	11.060441	9.157266	19.624730	28.841294	13.617304	17.698965
2019	11.569439	9.485989	20.147939	28.543263	13.304715	16.948655
2020	11.918015	9.704302	20.940185	28.368030	12.315390	16.754078
2021	12.275914	9.430825	21.071535	28.516758	12.343355	16.361612

Show code cell content

Hide code cell content

columns2 = [
    "High school",
    "Bachelor",
    "Some college",
    "No diploma",
    "Advanced",
    "Associate",
]

left = [
    "High school",
    "Some college",
    "No diploma",
]

Show code cell source

Hide code cell source

nudge = {"No diploma": 0, "Advanced": -0.2, "Associate": -0.2}

for column in xtab.columns:
    series = xtab[column]
    series.plot(label="", alpha=0.6)
    if column in left:
        x = series.index[0] - 0.3
        y = series.values[0] + nudge.get(column, 0) - 0.3
        plt.text(x, y, column, ha="right")
    else:
        x = series.index[-1] + 0.3
        y = series.values[-1] + nudge.get(column, 0) - 0.3
        plt.text(x, y, column, ha="left")


decorate(
    xlabel="Year",
    ylabel="Percent",
    xlim=[1988, 2022],
    title="Percent of labor force at each education level",
)
plt.xticks([2000, 2010, 2020])

([<matplotlib.axis.XTick at 0x753865f72980>,
  <matplotlib.axis.XTick at 0x75386619bfa0>,
  <matplotlib.axis.XTick at 0x753865f8ed70>],
 [Text(2000, 0, '2000'), Text(2010, 0, '2010'), Text(2020, 0, '2020')])

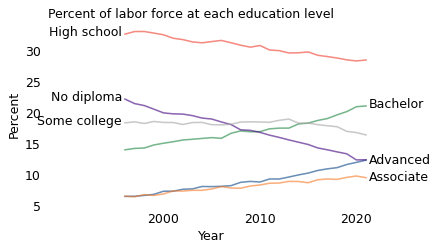
Compared to 1996, people in 2021 have more education. The groups with associate degrees, bachelor’s degrees, or advanced degrees have grown by 3-7 percentage points. Meanwhile, the groups with no diploma, high school, or some college have shrunk by 2-10 percentage points.

So the overall increase in real wages is driven by changes in education levels, not by higher wages at any level. For example, a person with a bachelor’s degree in 2021 makes less money, on average, than a person with a bachelor’s degree in 1996. But a random person in 2021 is more likely to have a bachelor’s degree (or more) than a person in 1996, so they make more money, on average.

Show code cell content

Hide code cell content

xtab.loc[2021] - xtab.loc[1996]

degree
Advanced        5.868831
Associate       3.005632
Bachelor        7.116409
High school    -4.194782
No diploma     -9.837951
Some college   -1.958139
dtype: float64

In both examples so far, the explanation for Simpson’s paradox is that the population is a mixture of groups and the proportions of the mixture change over time. In the GSS examples, the population is a mixture of generations, and the older generations are replaced by younger generations. In the CPS example, the population is a mixture of education levels, and the fraction of people at each level changes over time.

But Simpson’s paradox does not require the variable on the \(x\) axis to be time. More generally, it can happen with any variables on the \(x\) and \(y\) axes and any set of groups. To demonstrate, let’s look at an example that doesn’t depend on time.

10.3. Penguins

In 2014 a team of biologists published measurements they collected from three species of penguins living near the Palmer Research Station in Antarctica. For 344 penguins, the dataset includes body mass, flipper length, and the length and depth of their beaks: more specifically, the part of the beak called the culmen.

This dataset has become popular with machine learning experts because it is a fun way to demonstrate all kinds of statistical methods, especially classification algorithms.

Allison Horst, an environmental scientist who helped make this dataset freely available, used it to demonstrate Simpson’s paradox. The following figure shows the example she discovered:

Show code cell content

Hide code cell content

df = pd.read_csv(filename)
df.shape

(344, 17)

Show code cell content

Hide code cell content

def shorten(species):
    """Select the first word from a string."""
    return species.split()[0]


df["Species2"] = df["Species"].apply(shorten)

Show code cell content

Hide code cell content

var1 = "Flipper Length (mm)"
var2 = "Culmen Length (mm)"
var3 = "Culmen Depth (mm)"
var4 = "Body Mass (g)"

Show code cell content

Hide code cell content

from utils import Or70, Pu50, Gr30

colors = [Or70, Pu50, Gr30]
markers = ["s", "o", "^"]

Show code cell content

Hide code cell content

def scatterplot(df, var1, var2):
    """Make a scatter plot grouped by species.
    
    df: DataFrame with penguin data
    var1: name of variable for x-axis
    var2: name of variable for y-axis
    """
    grouped = df.groupby("Species2")
    i = 0
    for species, group in grouped:
        plt.plot(
            group[var1],
            group[var2],
            markers[i],
            color=colors[i],
            label=species,
            alpha=0.2,
        )
        i += 1

    decorate(xlabel=var1, ylabel=var2)
    plt.legend(loc="upper left", bbox_to_anchor=(0.98, 1.0))
    plt.tight_layout()

Show code cell content

Hide code cell content

def plot_line(group, result, **options):
    """Plot a linear regression line.

    group: DataFrame
    result: linear regression result
    """
    xs = group[var2].min(), group[var2].max()
    ys = np.array(xs) * result.slope + result.intercept
    plt.plot(xs, ys, alpha=0.5, **options)

Show code cell source

Hide code cell source

from scipy.stats import linregress

scatterplot(df, var2, var3)

data = df.dropna(subset=[var2, var3])
grouped = data.groupby("Species2")
i = 0
for species, group in grouped:
    result = linregress(group[var2], group[var3])
    plot_line(group, result, color=colors[i])
    i += 1

result = linregress(data[var2], data[var3])
plot_line(data, result, ls=":", color="gray")

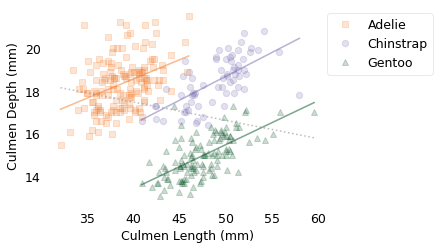
Each marker represents the culmen length and depth of an individual penguin. The different marker shapes represent different species: Adélie, Chinstrap, and Gentoo. The solid lines are the lines of best fit within each species; in all three, there is a positive correlation between length and depth. The dotted line shows the line of best fit among all of the penguins; between species, there is a negative correlation between length and depth.

In this example, the correlation within species has some meaning: most likely, length and depth are correlated because both are correlated with body size. Bigger penguins have bigger beaks.

However, when we combine samples from different species and find that the correlation of these variables is negative, that’s a statistical artifact. It depends on the species we choose and how many penguins of each species we measure. So it doesn’t really mean anything.

Show code cell content

Hide code cell content

for species, group in grouped:
    result = linregress(group[var2], group[var3])
    print(species, result.slope)

result = linregress(data[var2], data[var3])
print("overall", result.slope)

Adelie 0.178834349642578
Chinstrap 0.2222117240036715
Gentoo 0.20484434062147577
overall -0.08502128077717656

These results are puzzling only if you think the trend within groups is necessarily the same as the the trend between groups. Once you realize that’s not true, the paradox is resolved.

Penguins might be interesting, but dogs take Simpson’s paradox to a new level. In 2007, a team of biologists at Leiden University in the Netherlands and the Natural History Museum in Berne, Switzerland described the unusual case of one Simpson’s paradox nested inside another. They observe:

• When we compare species, there is a positive correlation between weight and lifespan: in general, bigger animals live longer.

• However, when we compare dog breeds, there is a negative correlation: bigger breeds have shorter lives, on average.

• However, if we compare dogs within a breed, there is a positive correlation again: a bigger dog is expected to live longer than a smaller dog of the same breed.

In summary, elephants live longer than mice, Chihuahuas live longer than Great Danes, and big beagles live longer than small beagles. The trend is different at the level of species, breed, and individual because the relationship at each level is driven by different biological processes.

These results are puzzling only if you think the trend within groups is necessarily the same as the the trend between groups. Once you realize that’s not true, the paradox is resolved.

10.4. Simpson’s Prescription

Some of the most bewildering examples of Simpson’s paradox come up in medicine, where a treatment might prove to be effective for men, effective for women, and ineffective or harmful for people. To understand examples like that, let’s start with an analogous example from the General Social Survey.

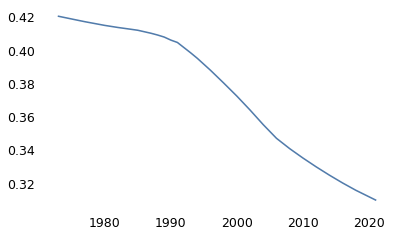
Since 1973, the GSS has asked respondents, “Is there any area right around here–that is, within a mile–where you would be afraid to walk alone at night?” Out of more than 37,000 people who have answered this question, about 38% said “Yes”.

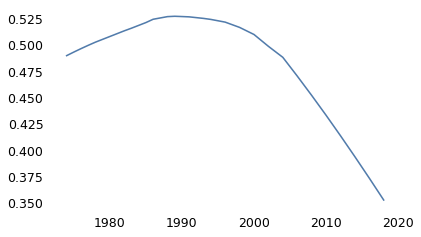
Since 1974, they have also asked, “Should divorce in this country be easier or more difficult to obtain than it is now?” About 49% of the respondents said it should be more difficult.

Show code cell content

Hide code cell content

gss["divlaw"].notna().sum()

37489

Show code cell content

Hide code cell content

(gss["divlaw"].dropna() == 2).mean()

0.48926351729840756

Show code cell source

Hide code cell source

xtab = pd.crosstab(gss["year"], gss["divlaw"], normalize="index")
plot_series_lowess(xtab[2])

Show code cell content

Hide code cell content

gss["fear"].notna().sum()

43573

Show code cell content

Hide code cell content

(gss["fear"].dropna() == 1).mean()

0.38328781584926447

Show code cell source

Hide code cell source

xtab = pd.crosstab(gss["year"], gss["fear"], normalize="index")
plot_series_lowess(xtab[1])

Now, if you had to guess, would you expect these responses to be correlated; that is, do you think someone who says they are afraid to walk alone at night might be more likely to say divorce should be more difficult? As it turns out, they are slightly correlated:

• Of people who said they are afraid, about 50% said divorce should be more difficult.

• Of people who said they are not afraid, about 49% said divorce should be more difficult.

However, there are several reasons we should not take this correlation too seriously:

• The difference between the groups is too small to make any real difference, even if it were valid;

• It combines results from 1974 to 2018, so it ignores the changes in both responses over that time; and

• It is actually an artifact of Simpson’s paradox.

To explain the third point, let’s look at responses from men and women separately. The following figure shows this breakdown.

Show code cell content

Hide code cell content

# This example doesn't work with the new 2021 data.
# Examples of Simpson's paradox are not always robust, but the
# point of this example is that it existed at a point in time.

gss = pd.read_hdf("gss_simpson.hdf", "gss")
gss.shape

(68846, 214)

Show code cell content

Hide code cell content

data = gss.dropna(subset=["fear"]).copy()

Show code cell content

Hide code cell content

data = data.replace({"fear": {2: 0}})
data["fear"].value_counts()

fear
0.0    26872
1.0    16701
Name: count, dtype: int64

Show code cell content

Hide code cell content

data = data.replace({"sex": {1: "Male", 2: "Female"}})
data["sex"].value_counts()

sex
Female    23420
Male      20011
Name: count, dtype: int64

Show code cell content

Hide code cell content

from utils import make_pivot_table

xvarname = "fear"
yvarname = "divlaw"
gvarname = "sex"
yvalue = 2

series, table = make_pivot_table(data, xvarname, yvarname, gvarname, yvalue)
series

fear
0.0    48.567299
1.0    50.683683
Name: all, dtype: float64

Show code cell source

Hide code cell source

table

sex	Female	Male
fear
0.0	50.795290	47.008671
1.0	51.736295	47.706879

Show code cell content

Hide code cell content

series

fear
0.0    48.567299
1.0    50.683683
Name: all, dtype: float64

Show code cell source

Hide code cell source

from utils import anchor_legend

table["Female"].plot(color="C1")
table["Male"].plot(ls="--", color="C0")

series.plot(ls=":", color="gray", label="Overall")
plt.plot(0, series[0], "s", color="gray")
plt.plot(1, series[1], ">", color="gray")

title = "Should divorce be easier to obtain?"
decorate(xlabel="Afraid at night", ylabel="Percent saying yes", title=title)
plt.xticks([0, 1], ["No", "Yes"])
anchor_legend(1.02, 1.02)
None

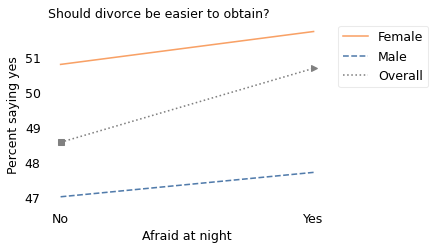
Among women, people who are afraid are less likely to say divorce should be difficult. And among men, people who are afraid are also less likely to say divorce should be difficult (very slightly). In both groups, the correlation is negative, but when we put them together, the correlation is positive. People who are afraid are more likely to say divorce should be difficult.

As with the other examples of Simpson’s paradox, this might seem to be impossible. But as with the other examples, it is not.

The key is to realize that there is a correlation between the sex of the respondent and their responses to both questions. In particular, of the people who said they are not afraid, 41% are female; of the people who said they are afraid, 74% are female. You can actually see these proportions in the figure:

• On the left, the square marker is 41% of the way between the male and female proportions.

• On the right, the triangle marker is 74% of the way between the male and female proportions.

In both cases, the overall proportion is a mixture of the male and female proportions. But it is a different mixture on the left and right. That’s why Simpson’s paradox is possible.

Show code cell source

Hide code cell source

xtab = pd.crosstab(data["fear"], data["sex"], normalize="index")
xtab

sex	Female	Male
fear
0.0	0.420412	0.579588
1.0	0.730517	0.269483

With this example under our belts, we are ready to take on one of the best-known examples of Simpson’s paradox. It comes from a paper, published in 1986 by researchers at St Paul’s Hospital in London, that compared two treatments for kidney stones: (A) open surgery and (B) percutaneous nephrolithotomy. For our purposes, it doesn’t matter what these treatments are; I’ll just call them A and B.

Among 350 patients who received Treatment A, 78% had a positive outcome; among another 350 patients who received Treatment B, 83% had a positive outcome. So it seems like Treatment B is better.

Show code cell content

Hide code cell content

index = [0, 1]
series = pd.Series([78, 83], index=index)
series

0    78
1    83
dtype: int64

Show code cell source

Hide code cell source

columns = ["Small", "Large"]
numer = pd.DataFrame([[81, 192], [234, 55]], index=index, columns=columns)
numer

	Small	Large
0	81	192
1	234	55

Show code cell source

Hide code cell source

denom = pd.DataFrame([[87, 263], [270, 80]], index=index, columns=columns)
denom

	Small	Large
0	87	263
1	270	80

Show code cell content

Hide code cell content

denom.T.sum()

0    350
1    350
dtype: int64

Show code cell content

Hide code cell content

series = numer.T.sum() / denom.T.sum() * 100
series

0    78.000000
1    82.571429
dtype: float64

However, when they split the patients into groups, they found that the results were reversed:

• Among patients with relatively small kidney stones, Treatment A was better, with a success rate of 93% compared to 86%.

• Among patients with larger kidney stones, Treatment A was better again, with a success rate of 73% compared to 69%.

The following figure shows these results in graphical form.

Show code cell source

Hide code cell source

table = numer / denom * 100
table

	Small	Large
0	93.103448	73.003802
1	86.666667	68.750000

Show code cell source

Hide code cell source

table["Small"].plot(color="C1")
table["Large"].plot(ls="--", color="C0")

series.plot(ls=":", color="gray", label="Overall")
plt.plot(0, series[0], "s", color="gray")
plt.plot(1, series[1], ">", color="gray")

decorate(
    xlabel="Treatment",
    ylabel="Percent",
    title="Kidney stone positive outcomes",
)
plt.xticks([0, 1], ["A", "B"])
anchor_legend(1.02, 1.02)
None

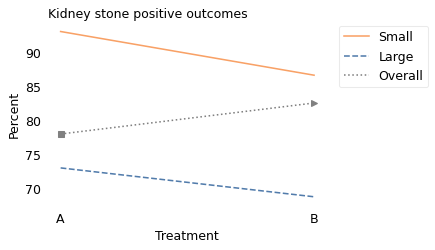
This figure resembles the previous one because the explanation is the same in both cases: the overall percentages, indicated by the square and triangle markers, are mixtures of the percentages from the two groups. But they are different mixtures on the left and right.

For medical reasons, patients with larger kidney stones were more likely to receive Treatment A; patients with smaller kidney stones were more likely to receive Treatment B.

As a result, among people who received Treatment A, 75% had large kidney stones, which is why the square marker on the left is closer to the Large group. And among people who received Treatment B, 77% had small kidney stones, which is why the triangle marker is closer to the Small group.

Show code cell source

Hide code cell source

props = denom.T / denom.T.sum()
props

	0	1
Small	0.248571	0.771429
Large	0.751429	0.228571

I hope this explanation makes sense, but even if it does, you might wonder how to choose a treatment. Suppose you are a patient and your doctor explains:

• For someone with a small kidney stone, Treatment A is better.

• For someone with a large kidney stone, Treatment A is better.

• But overall, Treatment B is better.

Which treatment should you choose? Other considerations being equal, you should choose A because it has a higher chance of success for any patient, regardless of stone size. The apparent success of B is a statistical artifact, the result of two causal relationships:

• Smaller stones are more likely to get Treatment B.

• Smaller stones are more likely to lead to a good outcome.

Looking at the overall results, Treatment B only looks good because it is used for easier cases; Treatment A only looks bad because it is used for the hard cases. If you are choosing a treatment, you should look at the results within the groups, not between the groups.

10.5. Do vaccines work? Hint: yes.

Now that we have mastered Simpson’s paradox, let’s get back to the example from the beginning of the chapter, the newsletter that went viral with the claim that “Vaccinated English adults under 60 are dying at twice the rate of unvaccinated people the same age”.

The newsletter includes a graph based on data from the U.K. Office for National Statistics. I downloaded the same data and replicated the graph, which looks like this:

Show code cell content

Hide code cell content

# https://substackcdn.com/image/fetch/f_auto,q_auto:good,fl_progressive:steep/https%3A%2F%2Fbucketeer-e05bbc84-baa3-437e-9518-adb32be77984.s3.amazonaws.com%2Fpublic%2Fimages%2Fbdca5329-b20b-4518-a733-fff84cc22124_1098x681.png

Show code cell content

Hide code cell content

# https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/datasets/deathsbyvaccinationstatusengland
# https://www.ons.gov.uk/file?uri=/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/datasets/deathsbyvaccinationstatusengland/deathsoccurringbetween2januaryand24september2021/datasetfinalcorrected3.xlsx

Show code cell source

Hide code cell source

df = pd.read_excel(
    filename,
    sheet_name="Table 4",
    skiprows=3,
    skipfooter=12,
)
df.tail()

	Week ending	Week number	Vaccination status	Age group	Number of deaths	Population	Percentage of total age-group population	Age-specific rate per 100,000	Unnamed: 8	Lower confidence limit	Upper confidence limit
603	2021-09-17	37	Second dose	80+	4000	2437192	96.3	164.1	NaN	159.1	169.3
604	2021-09-24	38	Second dose	10-59	400	17924346	66.4	2.2	NaN	2	2.5
605	2021-09-24	38	Second dose	60-69	638	4973647	93.8	12.8	NaN	11.9	13.9
606	2021-09-24	38	Second dose	70-79	1553	4171936	96.3	37.2	NaN	35.4	39.1
607	2021-09-24	38	Second dose	80+	3839	2439328	96.3	157.4	NaN	152.4	162.4

Show code cell content

Hide code cell content

df = df.replace({"Age-specific rate per 100,000": {":": np.nan}})

Show code cell content

Hide code cell content

df.columns

Index(['Week ending', 'Week number', 'Vaccination status', 'Age group',
       'Number of deaths', 'Population',
       'Percentage of total age-group population',
       'Age-specific rate per 100,000', 'Unnamed: 8', 'Lower confidence limit',
       'Upper confidence limit'],
      dtype='object')

Show code cell content

Hide code cell content

table = df.pivot_table(
    index="Week ending",
    columns=["Vaccination status", "Age group"],
    values="Age-specific rate per 100,000",
    aggfunc="median",
)

Show code cell source

Hide code cell source

table.head()

Vaccination status	21 days or more after first dose				Second dose				Unvaccinated				Within 21 days of first dose
Age group	10-59	60-69	70-79	80+	10-59	60-69	70-79	80+	10-59	60-69	70-79	80+	10-59	60-69	70-79	80+
Week ending
2021-01-08	NaN	NaN	NaN	190.1	NaN	NaN	NaN	8.1	3.7	27.3	69.8	413.4	0.7	10.8	32.6	84.5
2021-01-15	2.7	NaN	104.3	186.8	NaN	NaN	NaN	32.8	4.0	30.1	78.8	645.1	1.9	19.7	25.8	100.6
2021-01-22	2.0	7.5	107.2	175.7	NaN	NaN	NaN	52.8	4.1	30.8	95.5	1198.0	1.7	21.5	25.4	122.0
2021-01-29	2.3	14.4	65.0	152.3	NaN	NaN	NaN	53.4	3.7	29.2	112.2	1571.9	1.8	18.3	26.3	180.9
2021-02-05	1.5	15.0	59.9	157.5	NaN	NaN	NaN	64.7	3.6	26.5	168.2	1456.1	3.4	11.9	22.8	223.0

Show code cell content

Hide code cell content

recent = table.index >= pd.Timestamp("2021-3-19")

Show code cell source

Hide code cell source

table[recent]["Second dose", "10-59"].plot(color="C1", ls="-", label="Vaccinated")
table[recent]["Unvaccinated", "10-59"].plot(color="C0", ls="--", label="Unvaccinated")

plt.margins(x=0.1, tight=False)
decorate(
    xlabel="",
    ylabel="Weekly deaths per 100k",
    title="All cause death rates, ages 10–59",
    ylim=[0.1, 4.6],
    loc="upper right",
)

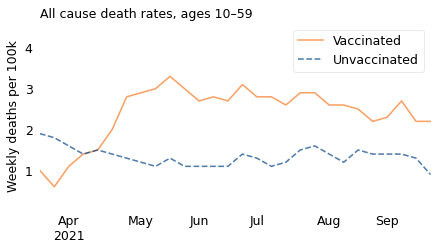
The lines show weekly death rates from all causes, per 100,000 people age 10-59, from March to September 2021. The solid line represents people who were fully vaccinated; the dashed line represents people who were unvaccinated.

The journalist I won’t name concludes: “Vaccinated people under 60 are twice as likely to die as unvaccinated people. And overall deaths in Britain are running well above normal. I don’t know how to explain this other than vaccine-caused mortality.” Well, I do.

There are two things wrong with his interpretation of the data:

• First, by choosing one age group and time interval, he has cherry-picked data that support his conclusion and ignored data that don’t.

• Second, because the data combine a wide range of ages, from 10 to 59, he has been fooled by Simpson’s paradox.

Let’s debunk one thing at a time. First, here’s what the graph looks like if we include the entire dataset, which starts in January:

Show code cell content

Hide code cell content

start = pd.Timestamp("2021-01-01")
end = pd.Timestamp("2021-09-30")

Show code cell content

Hide code cell content

options = dict(xlabel="", ylabel="Weekly deaths per 100k", xlim=[start, end])

Show code cell source

Hide code cell source

table["Second dose", "10-59"].plot(color="C1", label="Vaccinated")
table["Unvaccinated", "10-59"].plot(ls="--", label="Unvaccinated")

decorate(title="All cause death rates, ages 10–59", ylim=[0.1, 4.7], **options)

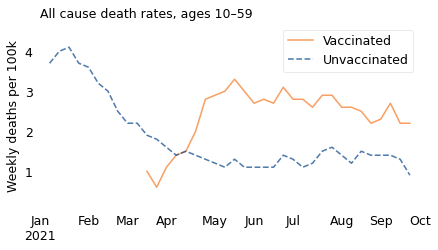
Overall death rates were “running well above normal” in January and February, when almost no one in the 10-59 age range had been vaccinated. Those deaths cannot have been caused by the vaccine; in fact, they were caused by a surge in the Alpha variant of COVID-19.

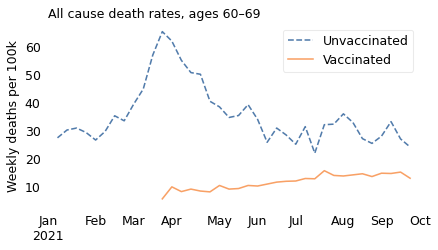
The unnamed journalist leaves out the time range that contradicts him; he also leaves out the age ranges that contradict him. In all of the older age ranges, death rates were consistently lower among people who had been vaccinated. The following figures show death rates for people in their 60s and 70s, and people over 80.

Show code cell source

Hide code cell source

ages = "60-69"
table["Unvaccinated", ages].plot(ls="--", label="Unvaccinated")
table["Second dose", ages].plot(label="Vaccinated")

decorate(title="All cause death rates, ages 60–69", **options)

Show code cell source

Hide code cell source

ages = "70-79"
table["Unvaccinated", ages].plot(ls="--", label="Unvaccinated")
table["Second dose", ages].plot(label="Vaccinated")

decorate(title="All cause death rates, ages 70–79", **options)

Show code cell source

Hide code cell source

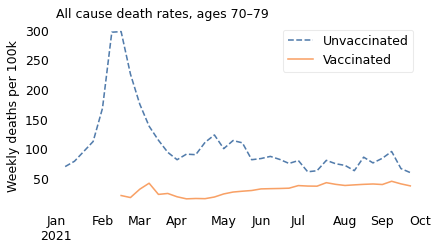
ages = "80+"
table["Unvaccinated", ages].plot(ls="--", label="Unvaccinated")
table["Second dose", ages].plot(label="Vaccinated")

decorate(title="All cause death rates, ages 80+", **options)

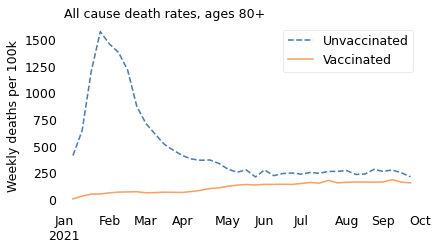
Notice that the \(y\) axes are on different scales; death rates are much higher in the older age groups.

Show code cell content

Hide code cell content

ages = "80+"
ratio = table["Unvaccinated", ages] / table["Second dose", ages]
ratio.iloc[:10]

Week ending
2021-01-08    51.037037
2021-01-15    19.667683
2021-01-22    22.689394
2021-01-29    29.436330
2021-02-05    22.505410
2021-02-12    19.391549
2021-02-19    16.596708
2021-02-26    11.674699
2021-03-05    11.043411
2021-03-12     9.223724
dtype: float64

In all of these groups, death rates are substantially lower for people who are vaccinated, which is what we expect from a vaccine that has been shown in large clinical trials to be safe and effective.

So what explains the apparent reversal among people between 10 and 59 years old? It is a statistical artifact caused by Simpson’s paradox. Specifically, it is caused by two correlations:

• Within this age group, older people were more likely to be vaccinated, and

• Older people were more likely to die of any cause, just because they are older.

Both of these correlations are strong. For example, at the beginning of August, about 88% of people at the high end of this age range had been vaccinated; none of the people at the low end had. And the death rate for people at the high end was 54 times higher than for people at the low end.

To show that these correlations are strong enough to explain the observed difference in death rates, I will follow an analysis by epidemiologist Jeffrey Morris, who refuted the unreliable journalist’s claims within days of their publication. He divides the excessively wide 10-59 year age group into 10 groups, each 5 years wide.

To estimate normal, pre-pandemic death rates in these groups, he uses 2019 data from the U.K. Office of National Statistics. To estimate the vaccination rate in each group, he uses data from the coronavirus dashboard provided by the U.K. Health Security Agency. Finally, to estimate the fraction of people in each age group, he uses data from a web site called PopulationPyramid, which organizes and publishes data from the United Nations Department of Economic and Social Affairs. Not to get lost in the details, these are all reliable data sources.

Combining these datasets, Morris is able to compute the distribution of ages in the vaccinated and unvaccinated groups at the beginning of August 2021 (choosing a point near the middle of the interval in the original graph). The following figure shows the results.

Show code cell content

Hide code cell content

index = [
    "10-14",
    "15-19",
    "20-24",
    "25-29",
    "30-34",
    "35-39",
    "40-44",
    "45-49",
    "50-54",
    "55-59",
]

Show code cell content

Hide code cell content

rate = [8.8, 23.1, 39.1, 48.4, 66.9, 97.3, 143.3, 219.6, 321.5, 478.2]
pct_vax = [0, 26.7, 59.6, 59.7, 63.3, 63.3, 74.6, 80.5, 85.6, 88.2]
pct_pop = [5.9, 5.5, 6.2, 6.8, 6.7, 6.6, 6.0, 6.6, 7.0, 6.6]

Show code cell content

Hide code cell content

rate[-1] / rate[0]

54.340909090909086

Show code cell source

Hide code cell source

sheet = pd.DataFrame(dict(rate=rate, pct_vax=pct_vax, pct_pop=pct_pop), index)
sheet

	rate	pct_vax	pct_pop
10-14	8.8	0.0	5.9
15-19	23.1	26.7	5.5
20-24	39.1	59.6	6.2
25-29	48.4	59.7	6.8
30-34	66.9	63.3	6.7
35-39	97.3	63.3	6.6
40-44	143.3	74.6	6.0
45-49	219.6	80.5	6.6
50-54	321.5	85.6	7.0
55-59	478.2	88.2	6.6

Show code cell source

Hide code cell source

sheet["pct_pop"] /= sheet["pct_pop"].sum()
sheet

	rate	pct_vax	pct_pop
10-14	8.8	0.0	0.092332
15-19	23.1	26.7	0.086072
20-24	39.1	59.6	0.097027
25-29	48.4	59.7	0.106416
30-34	66.9	63.3	0.104851
35-39	97.3	63.3	0.103286
40-44	143.3	74.6	0.093897
45-49	219.6	80.5	0.103286
50-54	321.5	85.6	0.109546
55-59	478.2	88.2	0.103286

Show code cell source

Hide code cell source

sheet["pct_vax_age"] = sheet["pct_pop"] * sheet["pct_vax"]
sheet["pct_vax_age"] /= sheet["pct_vax_age"].sum()
sheet

	rate	pct_vax	pct_pop	pct_vax_age
10-14	8.8	0.0	0.092332	0.000000
15-19	23.1	26.7	0.086072	0.037419
20-24	39.1	59.6	0.097027	0.094159
25-29	48.4	59.7	0.106416	0.103444
30-34	66.9	63.3	0.104851	0.108069
35-39	97.3	63.3	0.103286	0.106456
40-44	143.3	74.6	0.093897	0.114054
45-49	219.6	80.5	0.103286	0.135382
50-54	321.5	85.6	0.109546	0.152684
55-59	478.2	88.2	0.103286	0.148332

Show code cell source

Hide code cell source

sheet["pct_novax_age"] = sheet["pct_pop"] * (100 - sheet["pct_vax"])
sheet["pct_novax_age"] /= sheet["pct_novax_age"].sum()
sheet

	rate	pct_vax	pct_pop	pct_vax_age	pct_novax_age
10-14	8.8	0.0	0.092332	0.000000	0.239297
15-19	23.1	26.7	0.086072	0.037419	0.163513
20-24	39.1	59.6	0.097027	0.094159	0.101592
25-29	48.4	59.7	0.106416	0.103444	0.111147
30-34	66.9	63.3	0.104851	0.108069	0.099730
35-39	97.3	63.3	0.103286	0.106456	0.098241
40-44	143.3	74.6	0.093897	0.114054	0.061812
45-49	219.6	80.5	0.103286	0.135382	0.052199
50-54	321.5	85.6	0.109546	0.152684	0.040883
55-59	478.2	88.2	0.103286	0.148332	0.031587

Show code cell source

Hide code cell source

from empiricaldist import Pmf

pmf_novax = Pmf(sheet["pct_novax_age"], copy=True)
pmf_vax = Pmf(sheet["pct_vax_age"], copy=True)

pmf_novax.plot(ls="--", color="C4", label="Unvaccinated")
pmf_vax.plot(color="C2", label="Vaccinated")

decorate(
    xlabel="Age group",
    ylabel="Fraction of population",
    title="Distribution of ages",
    ylim=[0, 0.26],
)

Show code cell source

Hide code cell source

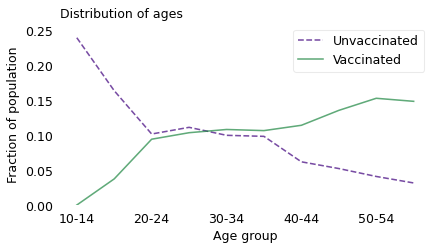
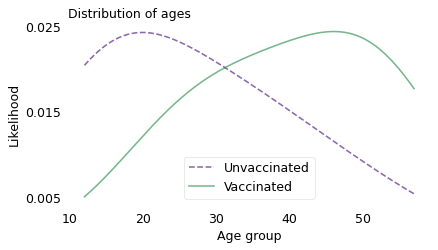
xs = [12, 17, 22, 27, 32, 37, 42, 47, 52, 57]

ps = sheet["pct_novax_age"]
sns.kdeplot(
    x=xs, weights=ps, cut=0, ls="--", color="C4", label="Unvaccinated", alpha=0.6
)

ps = sheet["pct_vax_age"]
sns.kdeplot(x=xs, weights=ps, cut=0, color="C2", label="Vaccinated", alpha=0.6)

decorate(
    xlabel="Age group",
    ylabel="Likelihood",
    title="Distribution of ages",
)
plt.yticks([0.005, 0.015, 0.025])

([<matplotlib.axis.YTick at 0x753864101f30>,
  <matplotlib.axis.YTick at 0x75386411fc70>,
  <matplotlib.axis.YTick at 0x75385c173550>],
 [Text(0, 0.005, '0.005'), Text(0, 0.015, '0.015'), Text(0, 0.025, '0.025')])

Show code cell content

Hide code cell content

pmf_vax.index = xs
pmf_novax.index = xs
pmf_vax.mean(), pmf_novax.mean()

(40.445446993711194, 26.68938091143594)

At this point during the rollout of the vaccines, people who were vaccinated were more likely to be at the high end of the age range, and people who were unvaccinated were more likely to be at the low end. Among the vaccinated, the average age was about 40; among the unvaccinated, it was 27.

Now, for the sake of this example, let’s imagine that there are no deaths due to COVID, and no deaths due to the vaccine. Based only on the distribution of ages and the death rates from 2019, we can compute the expected death rates for the vaccinated and unvaccinated groups. The ratio of these two rates is about 2.4.

So, prior to the pandemic, we would expect people with the age distribution of the vaccinated to die at a rate 2.4 times higher than people with the age distribution of the unvaccinated, just because they are older.

In reality, the pandemic increased the death rate in both groups, so the actual ratio was smaller, about 1.8. Thus, the results the journalist presented are not evidence that vaccines are harmful; as Morris concludes, they are “not unexpected, and can be fully explained by the Simpson’s paradox artifact”.

Show code cell source

Hide code cell source

sheet

	rate	pct_vax	pct_pop	pct_vax_age	pct_novax_age
10-14	8.8	0.0	0.092332	0.000000	0.239297
15-19	23.1	26.7	0.086072	0.037419	0.163513
20-24	39.1	59.6	0.097027	0.094159	0.101592
25-29	48.4	59.7	0.106416	0.103444	0.111147
30-34	66.9	63.3	0.104851	0.108069	0.099730
35-39	97.3	63.3	0.103286	0.106456	0.098241
40-44	143.3	74.6	0.093897	0.114054	0.061812
45-49	219.6	80.5	0.103286	0.135382	0.052199
50-54	321.5	85.6	0.109546	0.152684	0.040883
55-59	478.2	88.2	0.103286	0.148332	0.031587

Show code cell source

Hide code cell source

sheet["death_vax"] = sheet["rate"] * sheet["pct_vax_age"]
sheet["death_novax"] = sheet["rate"] * sheet["pct_novax_age"]
sheet

	rate	pct_vax	pct_pop	pct_vax_age	pct_novax_age	death_vax	death_novax
10-14	8.8	0.0	0.092332	0.000000	0.239297	0.000000	2.105810
15-19	23.1	26.7	0.086072	0.037419	0.163513	0.864387	3.777140
20-24	39.1	59.6	0.097027	0.094159	0.101592	3.681603	3.972229
25-29	48.4	59.7	0.106416	0.103444	0.111147	5.006692	5.379523
30-34	66.9	63.3	0.104851	0.108069	0.099730	7.229811	6.671929
35-39	97.3	63.3	0.103286	0.106456	0.098241	10.358164	9.558886
40-44	143.3	74.6	0.093897	0.114054	0.061812	16.344008	8.857590
45-49	219.6	80.5	0.103286	0.135382	0.052199	29.729969	11.462921
50-54	321.5	85.6	0.109546	0.152684	0.040883	49.087972	13.143951
55-59	478.2	88.2	0.103286	0.148332	0.031587	70.932358	15.104973

Show code cell content

Hide code cell content

sheet["death_vax"].sum(), sheet["death_novax"].sum()

(193.23496549826214, 80.03495027498823)

Show code cell content

Hide code cell content

sheet["death_vax"].sum() / sheet["death_novax"].sum()

2.4143822771718533

10.6. Debunk Redux

So far we have used only data that was publicly available in November 2021, but if we take advantage of more recent data, we can get a clearer picture of what was happening then and what has happened since.

In more recent reports, data from the U.K. Office of National Statistics are broken into smaller age groups. Instead of one group from ages 10 to 59, we have three groups from 18 to 39, 40 to 49, and 50 to 59.

Show code cell content

Hide code cell content

# https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/datasets/deathsbyvaccinationstatusengland
# https://www.ons.gov.uk/file?uri=/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/datasets/deathsbyvaccinationstatusengland/deathsoccurringbetween1january2021and31march2022/referencetable20220516accessiblecorrected.xlsx

Show code cell source

Hide code cell source

df = pd.read_excel(
    filename,
    sheet_name="Table 2",
    skiprows=3,
)
df.tail()

	Cause of Death	Year	Month	Age group	Vaccination status	Count of deaths	Person-years	Age-standardised mortality rate / 100,000 person-years	Noted as Unreliable	Lower confidence limit	Upper confidence limit
2200	Non-COVID-19 deaths	2022	March	90+	First dose, at least 21 days ago	57	191	29817.6	NaN	22582.1	38633
2201	Non-COVID-19 deaths	2022	March	90+	Second dose, less than 21 days ago	<3	7	x	NaN	x	x
2202	Non-COVID-19 deaths	2022	March	90+	Second dose, at least 21 days ago	515	1415	36402.2	NaN	33325.7	39686.4
2203	Non-COVID-19 deaths	2022	March	90+	Third dose or booster, less than 21 days ago	20	67	29992.6	NaN	18312.4	46323.7
2204	Non-COVID-19 deaths	2022	March	90+	Third dose or booster, at least 21 days ago	7024	36170	19419.5	NaN	18967.9	19879

Show code cell content

Hide code cell content

df.columns

Index(['Cause of Death', 'Year', 'Month', 'Age group', 'Vaccination status',
       'Count of deaths', 'Person-years',
       'Age-standardised mortality rate / 100,000 person-years',
       'Noted as Unreliable', 'Lower confidence limit',
       'Upper confidence limit'],
      dtype='object')

Show code cell content

Hide code cell content

df["date"] = pd.to_datetime(df["Year"].astype(str) + " " + df["Month"])

/tmp/ipykernel_1761109/3117688496.py:1: UserWarning: Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.
  df["date"] = pd.to_datetime(df["Year"].astype(str) + " " + df["Month"])

Show code cell content

Hide code cell content

rate = "Age-standardised mortality rate / 100,000 person-years"
df["rate"] = df[rate].replace("x", np.nan) / 52

Show code cell content

Hide code cell content

count = "Count of deaths"
df = df.replace({count: {"<3": np.nan}})

Show code cell content

Hide code cell content

all_cause = df["Cause of Death"] == "All causes"
all_cause_df = df[all_cause]
all_cause_df.shape

(735, 13)

Show code cell source

Hide code cell source

table = all_cause_df.pivot_table(
    index="date",
    columns=["Age group", "Vaccination status"],
    values="rate",
    aggfunc="median",
)
table

Age group	18-39							40-49			...	80-89			90+
Vaccination status	First dose, at least 21 days ago	First dose, less than 21 days ago	Second dose, at least 21 days ago	Second dose, less than 21 days ago	Third dose or booster, at least 21 days ago	Third dose or booster, less than 21 days ago	Unvaccinated	First dose, at least 21 days ago	First dose, less than 21 days ago	Second dose, at least 21 days ago	...	Third dose or booster, at least 21 days ago	Third dose or booster, less than 21 days ago	Unvaccinated	First dose, at least 21 days ago	First dose, less than 21 days ago	Second dose, at least 21 days ago	Second dose, less than 21 days ago	Third dose or booster, at least 21 days ago	Third dose or booster, less than 21 days ago	Unvaccinated
date
2021-01-01	2.305769	0.886538	NaN	NaN	NaN	NaN	1.338462	1.480769	1.457692	NaN	...	NaN	NaN	450.526923	559.213462	379.090385	128.263462	106.234615	NaN	NaN	1142.453846
2021-02-01	1.313462	2.232692	NaN	NaN	NaN	NaN	0.996154	2.419231	3.700000	NaN	...	NaN	NaN	994.521154	439.519231	460.546154	148.984615	300.221154	NaN	NaN	1736.271154
2021-03-01	1.767308	0.982692	NaN	NaN	NaN	NaN	0.836538	4.726923	2.678846	1.588462	...	NaN	NaN	478.028846	414.605769	628.298077	191.775000	197.580769	NaN	NaN	905.005769
2021-04-01	2.194231	0.875000	0.663462	1.051923	NaN	NaN	0.788462	4.421154	0.951923	1.342308	...	NaN	NaN	310.036538	722.825000	622.315385	274.011538	223.715385	NaN	NaN	573.459615
2021-05-01	1.573077	0.298077	1.278846	0.915385	NaN	NaN	0.719231	3.226923	0.909615	3.423077	...	NaN	NaN	205.926923	1423.846154	135.448077	310.394231	338.209615	NaN	NaN	441.151923
2021-06-01	1.353846	0.226923	1.398077	0.457692	NaN	NaN	1.013462	2.071154	2.248077	3.571154	...	NaN	NaN	207.298077	1352.734615	299.959615	308.330769	485.123077	NaN	NaN	436.778846
2021-07-01	0.688462	1.084615	1.525000	0.128846	NaN	NaN	1.200000	3.688462	1.842308	3.251923	...	NaN	NaN	219.240385	1203.386538	NaN	359.451923	488.507692	NaN	NaN	451.611538
2021-08-01	0.894231	NaN	0.982692	0.280769	NaN	NaN	1.109615	8.375000	5.334615	2.090385	...	NaN	NaN	225.351923	1080.765385	840.396154	368.871154	217.723077	NaN	NaN	485.823077
2021-09-01	1.225000	NaN	0.751923	0.234615	NaN	NaN	1.069231	9.867308	6.626923	2.532692	...	NaN	17.540385	219.619231	1101.913462	NaN	389.775000	227.242308	NaN	87.246154	419.742308
2021-10-01	1.569231	NaN	0.657692	NaN	1.409615	1.025000	0.971154	10.359615	NaN	2.361538	...	57.553846	51.503846	209.694231	1098.215385	1629.328846	569.080769	491.707692	217.957692	186.430769	463.415385
2021-11-01	1.407692	NaN	0.588462	0.655769	1.273077	0.965385	0.809615	5.736538	NaN	2.425000	...	84.676923	87.525000	234.880769	915.100000	1682.178846	854.875000	870.748077	306.765385	293.886538	469.390385
2021-12-01	1.082692	NaN	0.492308	NaN	1.178846	0.330769	1.186538	7.155769	NaN	2.775000	...	116.386538	180.213462	277.171154	975.467308	NaN	1261.742308	591.913462	394.207692	435.736538	541.403846
2022-01-01	0.861538	NaN	0.705769	NaN	0.555769	0.171154	0.675000	6.648077	NaN	4.094231	...	132.209615	288.563462	243.730769	1019.373077	1488.594231	1341.825000	413.482692	418.669231	531.225000	642.796154
2022-02-01	0.621154	NaN	0.575000	NaN	0.471154	NaN	0.442308	7.282692	NaN	3.023077	...	134.719231	352.348077	190.228846	741.442308	1879.340385	921.113462	986.521154	420.294231	639.675000	469.457692
2022-03-01	0.944231	NaN	0.453846	NaN	0.484615	NaN	0.486538	5.673077	NaN	2.842308	...	132.651923	248.367308	177.480769	653.894231	NaN	784.319231	NaN	411.732692	605.619231	384.192308

15 rows × 49 columns

Show code cell source

Hide code cell source

weight = all_cause_df.pivot_table(
    index="date",
    columns=["Age group", "Vaccination status"],
    values="Person-years",
    aggfunc="median",
)
weight

Age group	18-39							40-49			...	80-89			90+
Vaccination status	First dose, at least 21 days ago	First dose, less than 21 days ago	Second dose, at least 21 days ago	Second dose, less than 21 days ago	Third dose or booster, at least 21 days ago	Third dose or booster, less than 21 days ago	Unvaccinated	First dose, at least 21 days ago	First dose, less than 21 days ago	Second dose, at least 21 days ago	...	Third dose or booster, at least 21 days ago	Third dose or booster, less than 21 days ago	Unvaccinated	First dose, at least 21 days ago	First dose, less than 21 days ago	Second dose, at least 21 days ago	Second dose, less than 21 days ago	Third dose or booster, at least 21 days ago	Third dose or booster, less than 21 days ago	Unvaccinated
date
2021-01-01	4652.0	26531.0	245.0	1298.0	0.0	0.0	919726.0	3808.0	19144.0	230.0	...	0.0	0.0	73526.0	2868.0	13697.0	435.0	2480.0	0.0	0.0	18501.0
2021-02-01	42417.0	39726.0	1796.0	702.0	0.0	0.0	775131.0	30464.0	30705.0	1725.0	...	0.0	0.0	9636.0	20376.0	6965.0	3382.0	83.0	0.0	0.0	3233.0
2021-03-01	101611.0	63998.0	3920.0	10271.0	0.0	0.0	771499.0	77988.0	58483.0	3546.0	...	0.0	0.0	6529.0	26123.0	698.0	4282.0	4633.0	0.0	0.0	1970.0
2021-04-01	139889.0	32920.0	24262.0	35289.0	0.0	0.0	687679.0	124715.0	61689.0	18918.0	...	0.0	0.0	5050.0	7455.0	161.0	13980.0	13616.0	0.0	0.0	1502.0
2021-05-01	113834.0	54401.0	79347.0	52111.0	0.0	0.0	650418.0	166754.0	84731.0	60506.0	...	0.0	0.0	4821.0	1448.0	71.0	32341.0	2854.0	0.0	0.0	1408.0
2021-06-01	130731.0	148028.0	153165.0	53434.0	0.0	0.0	433521.0	164911.0	14535.0	130976.0	...	0.0	0.0	4441.0	644.0	38.0	34772.0	412.0	0.0	0.0	1294.0
2021-07-01	277344.0	99274.0	233284.0	61414.0	0.0	0.0	277646.0	64268.0	4330.0	247896.0	...	0.0	0.0	4441.0	457.0	23.0	36701.0	138.0	0.0	0.0	1295.0
2021-08-01	220983.0	20382.0	338822.0	127408.0	0.0	0.0	240885.0	21577.0	2046.0	355560.0	...	0.0	0.0	4344.0	370.0	11.0	37036.0	62.0	0.0	0.0	1271.0
2021-09-01	94196.0	10388.0	505837.0	88779.0	0.0	697.0	217515.0	14395.0	1297.0	369736.0	...	0.0	3627.0	4142.0	321.0	7.0	35489.0	25.0	0.0	573.0	1214.0
2021-10-01	67311.0	6356.0	615435.0	24779.0	3520.0	14868.0	215324.0	12672.0	994.0	370576.0	...	18622.0	62884.0	4219.0	292.0	12.0	22415.0	31.0	3168.0	11842.0	1237.0
2021-11-01	55034.0	4944.0	594332.0	12667.0	26066.0	22277.0	201381.0	10978.0	784.0	328710.0	...	104487.0	32240.0	4020.0	250.0	10.0	8868.0	27.0	19966.0	7466.0	1172.0
2021-12-01	47569.0	6244.0	489873.0	12516.0	63907.0	126969.0	199821.0	9915.0	945.0	202910.0	...	149236.0	9773.0	4082.0	227.0	11.0	3605.0	29.0	30572.0	3301.0	1186.0
2022-01-01	42878.0	6134.0	285156.0	9038.0	286671.0	125788.0	190750.0	9010.0	882.0	87018.0	...	161790.0	2083.0	4016.0	208.0	9.0	1845.0	19.0	34863.0	782.0	1164.0
2022-02-01	39248.0	2948.0	232464.0	4913.0	388129.0	19277.0	167539.0	8078.0	405.0	68465.0	...	148653.0	380.0	3598.0	179.0	4.0	1380.0	10.0	32413.0	141.0	1036.0
2022-03-01	42386.0	1460.0	249676.0	3968.0	454596.0	10328.0	183341.0	8695.0	164.0	72977.0	...	165318.0	201.0	3966.0	191.0	2.0	1415.0	7.0	36170.0	67.0	1141.0

15 rows × 49 columns

Show code cell content

Hide code cell content

all_cause_df["Vaccination status"].value_counts()

Vaccination status
Unvaccinated                                    105
First dose, less than 21 days ago               105
First dose, at least 21 days ago                105
Second dose, less than 21 days ago              105
Second dose, at least 21 days ago               105
Third dose or booster, less than 21 days ago    105
Third dose or booster, at least 21 days ago     105
Name: count, dtype: int64

Show code cell content

Hide code cell content

unvax_stat = ["Unvaccinated"]

vax_stat = [
    "Second dose, less than 21 days ago",
    "Second dose, at least 21 days ago",
    "Third dose or booster, less than 21 days ago",
    "Third dose or booster, at least 21 days ago",
]

Show code cell content

Hide code cell content

def weighted_sum(table, weight):
    """Weighted sum of table and weight.

    table: DataFrame
    weight: DataFrame

    returns: Series
    """
    # make sure that weight is 0 where table is NaN
    a = np.where(table.notna(), weight, 0)
    weight = pd.DataFrame(a, index=weight.index, columns=weight.columns)

    # normalize the weights rowwise
    total = weight.sum(axis=1)
    weight_norm = weight.divide(total, axis=0)

    # compute the weighted sum of table
    prod = table.fillna(0) * weight_norm
    return prod.sum(axis=1).replace(0, np.nan)

Show code cell content

Hide code cell content

def get_groups(frame, groups, status):
    """Select age groups and vax status.

    frame: DataFrame (table or weights)
    groups: list of string age group names
    status: list of string vax status

    returns: DataFrame
    """
    seq = [frame[group][status] for group in groups]
    return pd.concat(seq, axis=1)

Show code cell content

Hide code cell content

def make_plot(table, weight, groups):
    """Plot mortality for vaxed and unvaxed.

    table: DataFrame
    weight: DataFrame
    groups: list of string age groups
    """
    t = get_groups(table, groups, unvax_stat)
    w = get_groups(weight, groups, unvax_stat)
    unvax = weighted_sum(t, w)

    t = get_groups(table, groups, vax_stat)
    w = get_groups(weight, groups, vax_stat)
    vax = weighted_sum(t, w)

    ages = ",".join(groups)
    unvax.plot(ls="--", label="Unvaccinated")
    vax.plot(label="Vaccinated")

    decorate(
        xlabel="",
        ylabel="Weekly deaths per 100k",
        title=f"All cause death rates, ages {ages}",
    )

    # adjust the axes
    ax = plt.gca()
    low, high = plt.gca().get_ylim()
    plt.ylim(0, high)

    start = pd.Timestamp("2020-12-15")
    end = pd.Timestamp("2022-04-01")
    plt.xlim(start, end)

Show code cell source

Hide code cell source

# This figure shows what happens if we combine the youngest three groups,
# as in the original data
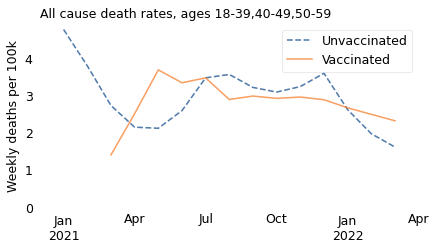
groups = ["18-39", "40-49", "50-59"]
make_plot(table, weight, groups)

Show code cell source

Hide code cell source

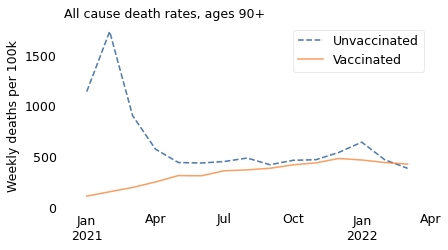
# the following figures look at the older age groups, which I won't present again

groups = ["90+"]
make_plot(table, weight, groups)

Show code cell source

Hide code cell source

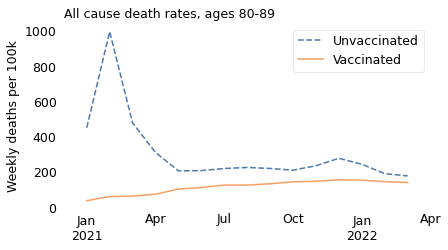
groups = ["80-89"]
make_plot(table, weight, groups)

Show code cell source

Hide code cell source

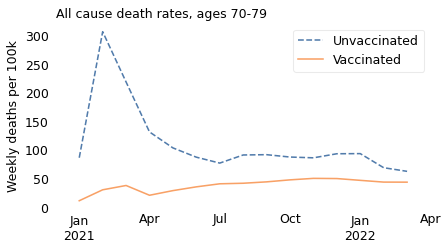
groups = ["70-79"]
make_plot(table, weight, groups)

Show code cell source

Hide code cell source

groups = ["60-69"]
make_plot(table, weight, groups)

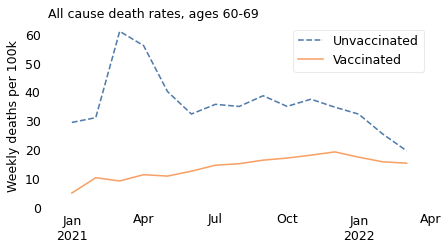
Let’s start with the oldest of these subgroups. Among people in their 50s, we see that the all-cause death rate was substantially higher among unvaccinated people over the entire interval from March 2021 to April 2022.

Show code cell source

Hide code cell source

groups = ["50-59"]
make_plot(table, weight, groups)
plt.ylim([0, 24])
plt.legend(loc="upper right")

<matplotlib.legend.Legend at 0x75385be1df60>

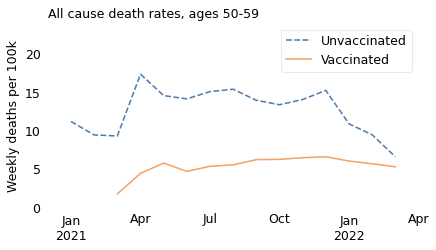
If we select people in their 40s, we see the same thing: death rates were higher for unvaccinated people over the entire interval.

Show code cell source

Hide code cell source

groups = ["40-49"]
make_plot(table, weight, groups)
plt.ylim([0, 7.8])
plt.legend(loc="upper right")

<matplotlib.legend.Legend at 0x7538682ecfd0>

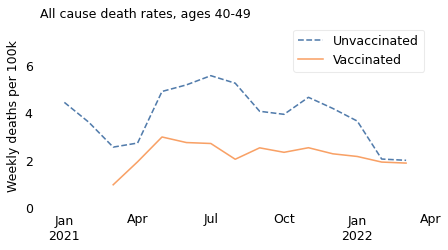
However, it is notable that death rates in both groups have declined since April or May 2021, and have nearly converged. Possible explanations include improved treatment for coronavirus disease and the decline of more lethal variants of the COVID virus. In the U.K., December 2021 is when the Delta variant was largely replaced by the Omicron variant, which is less deadly.

Finally, let’s see what happened in the youngest group, people aged 18 to 39.

Show code cell source

Hide code cell source

groups = ["18-39"]
make_plot(table, weight, groups)

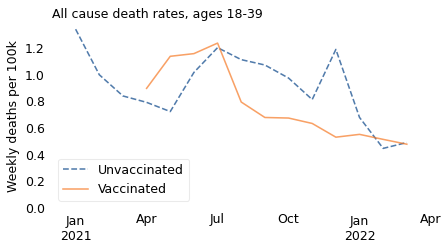
In this age group, like the others, death rates are generally higher among unvaccinated people. There are a few months where the pattern is reversed, but we should not take it too seriously because:

• Death rates in this age group are very low, less than 1 per 100,000 per week, vaccinated or not.

• The apparent differences between the groups are even smaller, and might be the result of random variation.

• Finally, this age group is still broad enough that the results are influenced by Simpson’s paradox. The vaccinated people in this group were older than the unvaccinated, and the older people in this group were about 10 times more likely to die, just because of their age.

In summary, the excess mortality among vaccinated people in 2021 is entirely explained by Simpson’s paradox. If we break the dataset into appropriate age groups, we see that death rates were higher among the unvaccinated in all age groups over the entire time from the rollout of the vaccine to the present. And we can conclude that the vaccine saved many lives.

Show code cell content

Hide code cell content

may = (df["Year"] == 2021) & (df["Month"] == "May")
may.sum()

147

Show code cell content

Hide code cell content

fully = df["Vaccination status"] == "Second dose, at least 21 days ago"
fully.sum()

315

Show code cell content

Hide code cell content

age = df["Age group"] == "18-39"
age.sum()

315

Show code cell source

Hide code cell source

df[may & fully & age]

	Cause of Death	Year	Month	Age group	Vaccination status	Count of deaths	Person-years	Age-standardised mortality rate / 100,000 person-years	Noted as Unreliable	Lower confidence limit	Upper confidence limit	date	rate
200	All causes	2021	May	18-39	Second dose, at least 21 days ago	52.0	79347	66.5	NaN	48.9	88.3	2021-05-01	1.278846
935	Deaths involving COVID-19	2021	May	18-39	Second dose, at least 21 days ago	NaN	79347	x	NaN	x	x	2021-05-01	NaN
1670	Non-COVID-19 deaths	2021	May	18-39	Second dose, at least 21 days ago	52.0	79347	66.5	NaN	48.9	88.3	2021-05-01	1.278846

Show code cell source

Hide code cell source

sheet

	rate	pct_vax	pct_pop	pct_vax_age	pct_novax_age	death_vax	death_novax
10-14	8.8	0.0	0.092332	0.000000	0.239297	0.000000	2.105810
15-19	23.1	26.7	0.086072	0.037419	0.163513	0.864387	3.777140
20-24	39.1	59.6	0.097027	0.094159	0.101592	3.681603	3.972229
25-29	48.4	59.7	0.106416	0.103444	0.111147	5.006692	5.379523
30-34	66.9	63.3	0.104851	0.108069	0.099730	7.229811	6.671929
35-39	97.3	63.3	0.103286	0.106456	0.098241	10.358164	9.558886
40-44	143.3	74.6	0.093897	0.114054	0.061812	16.344008	8.857590
45-49	219.6	80.5	0.103286	0.135382	0.052199	29.729969	11.462921
50-54	321.5	85.6	0.109546	0.152684	0.040883	49.087972	13.143951
55-59	478.2	88.2	0.103286	0.148332	0.031587	70.932358	15.104973

Show code cell content

Hide code cell content

mortality = sheet["rate"] / 52
mortality

10-14    0.169231
15-19    0.444231
20-24    0.751923
25-29    0.930769
30-34    1.286538
35-39    1.871154
40-44    2.755769
45-49    4.223077
50-54    6.182692
55-59    9.196154
Name: rate, dtype: float64

Show code cell content

Hide code cell content

mortality["55-59"], mortality["20-24"]

(9.196153846153846, 0.7519230769230769)

Show code cell content

Hide code cell content

mortality["55-59"] / mortality["20-24"]

12.230179028132993

Show code cell content

Hide code cell content

sheet.loc["55-59", "pct_vax"], sheet.loc["20-24", "pct_vax"]

(88.2, 59.6)

Show code cell content

Hide code cell content

sheet.loc["55-59", "pct_vax"] / sheet.loc["20-24", "pct_vax"]

1.4798657718120805

10.7. Lives saved

Show code cell source

Hide code cell source

df = pd.read_excel(
    filename,
    sheet_name="Table 2",
    skiprows=3,
)
df.tail()

	Cause of Death	Year	Month	Age group	Vaccination status	Count of deaths	Person-years	Age-standardised mortality rate / 100,000 person-years	Noted as Unreliable	Lower confidence limit	Upper confidence limit
2200	Non-COVID-19 deaths	2022	March	90+	First dose, at least 21 days ago	57	191	29817.6	NaN	22582.1	38633
2201	Non-COVID-19 deaths	2022	March	90+	Second dose, less than 21 days ago	<3	7	x	NaN	x	x
2202	Non-COVID-19 deaths	2022	March	90+	Second dose, at least 21 days ago	515	1415	36402.2	NaN	33325.7	39686.4
2203	Non-COVID-19 deaths	2022	March	90+	Third dose or booster, less than 21 days ago	20	67	29992.6	NaN	18312.4	46323.7
2204	Non-COVID-19 deaths	2022	March	90+	Third dose or booster, at least 21 days ago	7024	36170	19419.5	NaN	18967.9	19879

Show code cell content

Hide code cell content

df["date"] = pd.to_datetime(df["Year"].astype(str) + " " + df["Month"])

/tmp/ipykernel_1761109/3117688496.py:1: UserWarning: Could not infer format, so each element will be parsed individually, falling back to `dateutil`. To ensure parsing is consistent and as-expected, please specify a format.
  df["date"] = pd.to_datetime(df["Year"].astype(str) + " " + df["Month"])

Show code cell content

Hide code cell content

all_cause = df["Cause of Death"] == "All causes"
all_cause.sum()

735

Show code cell content

Hide code cell content

rate_col = "Age-standardised mortality rate / 100,000 person-years"
df = df.replace({rate_col: {"x": np.nan}})
df[rate_col].describe()

count     1447.000000
mean      6413.953766
std      12747.774742
min          0.900000
25%        122.400000
50%        835.700000
75%       6364.750000
max      97725.700000
Name: Age-standardised mortality rate / 100,000 person-years, dtype: float64

Show code cell content

Hide code cell content

def estimate_saved_lives(period):
    """Estimate lives saved by comparing actual deaths to possible deaths.
    
    period: DataFrame with vaccination status, deaths, population, and rates
    
    returns: number of lives saved (actual deaths - possible deaths)
    """
    index = period["Vaccination status"]
    deaths = pd.Series(period["Count of deaths"].values, index=index)
    pop = pd.Series(period["Person-years"].values, index=index)
    rate = pd.Series(period[rate_col].values, index=index)

    # choose the minimum rate among the fully vaccinated / boosted
    possible_rate = rate.iloc[4:].min() / 1e5
    actual_deaths = deaths["Unvaccinated"]
    possible_deaths = possible_rate * pop["Unvaccinated"]
    return actual_deaths - possible_deaths

Show code cell source

Hide code cell source

res = []
for name, period in df[all_cause].groupby(["Age group", "date"]):
    saved = estimate_saved_lives(period)
    res.append((name[0], name[1], saved))

saved_df = pd.DataFrame(res, columns=["Age group", "date", "saved"])
saved_df

	Age group	date	saved
0	18-39	2021-01-01	NaN
1	18-39	2021-02-01	NaN
2	18-39	2021-03-01	NaN
3	18-39	2021-04-01	31.750745
4	18-39	2021-05-01	-207.527970
...	...	...	...
100	90+	2021-11-01	106.893788
101	90+	2021-12-01	90.884232
102	90+	2022-01-01	135.587888
103	90+	2022-02-01	26.579092
104	90+	2022-03-01	-16.289241

105 rows × 3 columns

Show code cell content

Hide code cell content

series = saved_df.groupby("date")["saved"].sum()
series

date
2021-01-01    25602.785167
2021-02-01    14539.347887
2021-03-01     5751.205365
2021-04-01     2371.099972
2021-05-01     1081.724156
2021-06-01      904.974268
2021-07-01      922.228068
2021-08-01     1075.862092
2021-09-01     1603.805799
2021-10-01     1530.583100
2021-11-01     1353.284205
2021-12-01     1445.124507
2022-01-01     1108.678014
2022-02-01      469.170039
2022-03-01      286.239461
Name: saved, dtype: float64

Show code cell content

Hide code cell content

index = period["Vaccination status"]
deaths = pd.Series(period["Count of deaths"].values, index=index)
deaths

pop = pd.Series(period["Person-years"].values, index=index)
pop

rate = pd.Series(period[rate_col].values, index=index)
rate

boosted = "Third dose or booster, at least 21 days ago"
possible_rate = rate.iloc[4:].min() / 1e5
possible_rate

pop[boosted] * possible_rate

deaths[boosted]

actual_deaths = deaths["Unvaccinated"]

possible_deaths = possible_rate * pop["Unvaccinated"]
actual_deaths, possible_deaths

(228, 244.28924099999998)

10.8. Sources and related reading

• The General Social Survey (GSS) is a project of the University of Chicago’s independent research organization NORC, with primary financing from the National Science Foundation. Data is available from the GSS website.

• Floyd Norris wrote about changes in real wages in The New York Times (Norris, 2013). The following week, he wrote a blog article to respond to readers who thought he had made a mistake (Norris, 2013).

• The IPUMS CPS data is from the U.S. Census Bureau: Sarah Flood, Miriam King, Renae Rodgers, Steven Ruggles, J. Robert Warren, Daniel Backman, Annie Chen, Grace Cooper, Stephanie Richards, Megan Schouweiler, and Michael Westberry. Integrated Public Use Microdata Series, Current Population Survey: Version 11.0 [dataset]. Minneapolis, MN: IPUMS, 2023. https://doi.org/10.18128/D030.V11.0

• The penguin dataset was reported in “Ecological sexual dimorphism and environmental variability within a community of Antarctic penguins” (Gorman et al., 2014). Allison Horst pointed out the penguin paradox in the online documentation of the dataset.

• The nested Simpson’s paradox among dog breeds is described in “Do large dogs die young?” (Galis et al., 2007).

• The paper that evaluates treatments for kidney stones was published in 1986 in the British Medical Journal (Charig et al., 1986).

• Derek Thompson wrote about the misleading journalist in The Atlantic (Thompson, 2021). Jeffrey Morris debunks the misleading newsletter in a series of blog articles (Morris, 2021).

• Information about the prevalence of different COVID variants is from the U.K. Health Security Agency (U.K. Health Security Agency, 2022).

• The COVID data I used is from the U.K. Office for National Statistics (U.K. Office for National Statistics, 2022).

10.9. Open data, open discussion

Reflecting on this episode, we can identify several elements that went wrong. A journalist downloaded data he did not have the expertise to interpret correctly. He wrote about it in a newsletter that was published with no editorial review. Its spread was accelerated by a credulous podcaster who ignored numerous easily discoverable articles debunking its claims. And, given the circulation it achieved, it contributed to a body of vaccine misinformation that almost certainly caused preventable deaths.

All that is true; nevertheless, it is also important to consider the elements that went right.

First, the U.K. government collected reliable data about the pandemic and made it widely available. Other countries followed their example, albeit some more successfully than others. Groups like Our World in Data collected similar data from around the world and made it easier to use, which accelerated the ability of researchers to understand the pandemic, make predictions, and guide public policy decisions. This data saved lives.

Second, after the misleading newsletter was posted on November 20, dozens of articles debunked its claims within days. If you do a web search for the article today, the first page of results includes rebuttals published on November 21, 22, and 23.

Finally, even on social media sites that are infamous for spreading disinformation, public discussion of the article was not all bad. Simpson’s paradox is not easy to understand, but some of the explanations were very good. I think it’s a hopeful sign to see people grappling with statistical ideas in a public forum.

The marketplace of ideas will never be perfect, but this episode, which shows its weaknesses, also shows its strengths. We are better off when our decisions are guided by evidence and reason, but that is only possible if we have access to data and open spaces to discuss difficult ideas.

10.10. Israeli Data

This is an analysis I started with another dataset that demonstrates a Simpson’s paradox if you don’t separate age groups.

Downloaded from https://www.covid-datascience.com/post/israeli-data-how-can-efficacy-vs-severe-disease-be-strong-when-60-of-hospitalized-are-vaccinated

Originally from an Israeli government COVID dashboard with headings translated by Jeffrey S. Morris, director of the Biostatistics Division at the University of Pennsylvania.

https://www.dbei.med.upenn.edu/bio/jeffrey-s-morris-phd

Show code cell source

Hide code cell source

df = pd.read_excel(filename, skiprows=2).loc[0:9]
df.index = df["age group"]
del df["age group"]
df

	population unvax	population vax	population partial	proportion unvax	proportion vax	proportion partial	not vax	vax	partial vax	not vax per 100k	...	proportion of unvax	severe unvax	severe vax	severe partial vax	severe unvax per 100k	risk severe 20-29	severe vax 100k	severe parital vax per 1`00k	Efficacy severe	Efficacy severe partial
age group
12-15	383648.581384	184549.356223	49986.229689	0.620606	0.298535	0.080860	3083.0	172.0	363.0	803.6	...	0.294455	1	0	0.0	0.3	0.048387	0.0	0.0	1.000000	1.000000
16-19	127745.045528	429109.159348	26662.484316	0.218923	0.735385	0.045693	954.0	1710.0	85.0	746.8	...	0.098046	2	0	0.0	1.6	0.258065	0.0	0.0	1.000000	1.000000
20-29	265871.262336	991408.292865	43064.876957	0.204462	0.762420	0.033118	1805.0	5308.0	154.0	678.9	...	0.204059	4	0	0.0	1.5	0.241935	0.0	0.0	1.000000	1.000000
30-39	194213.423919	968837.047354	33911.882510	0.162255	0.809413	0.028332	1658.0	5565.0	127.0	853.7	...	0.149061	12	2	0.0	6.2	1.000000	0.2	0.0	0.967742	1.000000
40-49	145355.468255	927214.116050	26025.236593	0.132310	0.844000	0.023690	1147.0	5465.0	66.0	789.1	...	0.111562	24	9	1.0	16.5	2.661290	1.0	3.8	0.939394	0.769697
50-59	84545.028143	747949.291573	17472.118959	0.099469	0.879975	0.020556	721.0	4012.0	47.0	852.8	...	0.064889	34	22	0.0	40.2	6.483871	2.9	0.0	0.927861	1.000000
60-69	65204.929779	665716.790881	10668.163953	0.087926	0.897689	0.014386	455.0	3037.0	19.0	697.8	...	0.050046	50	58	3.0	76.7	12.370968	8.7	28.1	0.886571	0.633638
70-79	20512.376666	464336.324988	5885.500268	0.041799	0.946207	0.011993	237.0	1966.0	22.0	1155.4	...	0.015743	39	92	2.0	190.1	30.661290	19.8	34.0	0.895844	0.821147
80-89	12683.457148	208911.307272	3924.366750	0.056241	0.926357	0.017401	140.0	994.0	11.0	1103.8	...	0.009735	32	100	2.0	252.3	40.693548	47.9	51.0	0.810147	0.797860
90+	3132.059971	46601.941748	1764.112903	0.060819	0.904925	0.034256	61.0	264.0	7.0	1947.6	...	0.002404	16	18	2.0	510.9	82.403226	38.6	113.4	0.924447	0.778039

10 rows × 24 columns

Show code cell content

Hide code cell content

df.columns

Index(['population unvax', 'population vax', 'population partial',
       'proportion unvax', 'proportion vax', 'proportion partial', 'not vax',
       'vax', 'partial vax', 'not vax per 100k', 'vax per 100k',
       'partial vax 100k', 'Efficacy', 'Efficacy partial',
       'proportion of unvax', 'severe unvax', 'severe vax',
       'severe partial vax', 'severe unvax per 100k', 'risk severe 20-29',
       'severe vax 100k', 'severe parital vax per 1`00k', 'Efficacy severe',
       'Efficacy severe partial'],
      dtype='object')

Show code cell content

Hide code cell content

overall = df.sum()
overall

population unvax                1302911.633129
population vax                  5634633.628302
population partial               219364.972898
proportion unvax                       1.68481
proportion vax                        8.004906
proportion partial                    0.310284
not vax                                10261.0
vax                                    28493.0
partial vax                              901.0
not vax per 100k                        9629.5
vax per 100k                            4649.2
partial vax 100k                        3528.7
Efficacy                              4.770884
Efficacy partial                      6.030771
proportion of unvax                        1.0
severe unvax                               214
severe vax                                 301
severe partial vax                        10.0
severe unvax per 100k                   1096.3
risk severe 20-29                   176.822581
severe vax 100k                          119.1
severe parital vax per 1`00k             230.3
Efficacy severe                       9.352006
Efficacy severe partial                8.80038
dtype: object

Show code cell content

Hide code cell content

overall_risk_vax = overall["severe vax"] / overall["population vax"] * 1e5
overall_risk_vax

5.341962226046172

Show code cell content

Hide code cell content

overall_risk_unvax = overall["severe unvax"] / overall["population unvax"] * 1e5
overall_risk_unvax

16.4247516530378

Show code cell content

Hide code cell content

age_group = df.index
risk_vax = pd.Series(df["severe vax 100k"].values, index=age_group)
risk_unvax = pd.Series(df["severe unvax per 100k"].values, index=age_group)
risk_vax

age group
12-15     0.0
16-19     0.0
20-29     0.0
30-39     0.2
40-49     1.0
50-59     2.9
60-69     8.7
70-79    19.8
80-89    47.9
90+      38.6
dtype: float64

Show code cell content

Hide code cell content

table = pd.DataFrame(columns=["age_group"])

Probably Overthinking It

Copyright 2022 Allen Downey

The code in this notebook and utils.py is under the MIT license.