The Variability Hypothesis

This notebook demonstrates the use of resampling for hypothesis testing. I used it as part of a keynote at posit::conf 2024.

The variability hypothesis is the theory that males are generally more variable than females in both physical and psychological traits. It is a controversial claim, to put it mildly.

As a quick exploration of the topic – and a demonstration of bootstrap resampling – let’s see whether men are more variable than women in height. We’ll use the 2022 dataset from the Behavioral Risk Factor Surveillance System (BRFSS), which includes self-reported heights and weights for more than 400,000 respondents.

Click here to run this notebook on Colab.

try:
    import empiricaldist
except ImportError:
    !pip install empiricaldist

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

np.random.seed(42)
plt.rcParams["figure.dpi"] = 75
plt.rcParams["figure.figsize"] = [6, 3.5]

Data

The following function reads the data in an SAS export format, downloaded from the BRFSS website on August 1, 2024. It selects the columns we’ll use and writes the much smaller excerpt to an HDF file.

def write_hdf():
    """Read the SAS export file and write an HDF file."""
    brfss = pd.read_sas("LLCP2022.XPT.gz")
    columns = ["_SEX", "HTM4", "WTKG3", "_LLCPWT"]
    brfss[columns].to_hdf("LLCP2022.hdf5", key="brfss", complevel=6)

Rather than download the whole dataset, we can get just the excerpt.

from os.path import basename, exists


def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve

        local, _ = urlretrieve(url, filename)
        print("Downloaded " + local)


download("https://github.com/AllenDowney/ThinkStats/raw/v3/data/LLCP2022.hdf5")

Here are the first few rows.

brfss = pd.read_hdf("LLCP2022.hdf5", key="brfss")
brfss.describe()

	_SEX	HTM4	WTKG3	_LLCPWT
count	445132.000000	416480.000000	403054.000000	445132.000000
mean	1.529942	170.269057	8307.447039	594.856344
std	0.499103	10.717750	2144.817270	1134.837415
min	1.000000	91.000000	2268.000000	0.020464
25%	1.000000	163.000000	6804.000000	115.885991
50%	2.000000	170.000000	8074.000000	274.632388
75%	2.000000	178.000000	9525.000000	627.913694
max	2.000000	241.000000	29257.000000	54390.520926

The dataset includes self-reported heights for almost 200,000 mean and almost 220,000 women. Here are numbers of males and females with the shortest recorded heights.

xtab = pd.crosstab(brfss["HTM4"], brfss["_SEX"])
xtab.columns = ["Male", "Female"]
xtab.head()

	Male	Female
HTM4
91.0	7	17
92.0	0	1
95.0	1	0
97.0	1	3
99.0	1	0

And the tallest recorded heights.

xtab.tail()

	Male	Female
HTM4
226.0	9	2
229.0	4	1
234.0	4	0
236.0	1	0
241.0	4	1

According to the codebook, heights below 91 cm are set to 91 cm, and heights above 241 cm are set to 241 cm. Even so, some of the remaining values are likely to be errors. For example, the current tallest woman in the world is 234 cm, so the largest female height in the dataset, 241 cm, was probably reported or recorded incorrectly.

To draw a bootstrap sample from this DataFrame, we’ll use the following function.

def resample(df):
    """Draw a bootstrap sample.

    df: DataFrame

    returns: DataFrame
    """
    n = len(df)
    return df.sample(n, replace=True, weights="_LLCPWT")

Here’s a single sample we’ll use for testing.

sample = resample(brfss)

Difference in means

Before we test whether men are more variable than women, let’s warm up by confirming that men are taller than women, on average. We’ll use bootstrap resampling to estimate the sampling distribution of the difference in means. The following is a utility function that computes the difference between the first two elements of a sequence.

def diff(seq):
    """Difference between the first two elements of a sequence.

    seq: sequence

    returns: float
    """
    return np.diff(seq)[0]

We’ll use it to compute the difference in means in a sample, which is the “test statistic”.

def diff_means(sample):
    """Difference in average height (M minus F).

    sample: DataFrame with _SEX and HTM4 columns

    returns: float
    """
    grouped_heights = sample.groupby("_SEX")["HTM4"]
    return -diff(grouped_heights.mean())

The difference is defined so a positive value indicates that men are taller. Here an example using the bootstrapped sample.

diff_means(sample)

14.455796580284954

Men are about 14 cm taller than women, on average.

The following function takes a DataFrame and a function that computes a test statistic. It runs resample many times, computes the test statistic for each sample, and returns a list of test statistics.

def sampling_dist(df, test_stat, iters=201):
    """Generate bootstrap samples and compute test statistic.

    df: DataFrame
    test_stat: function that takes a DataFrame
    iters: number of samples

    returns: list of float
    """
    return [test_stat(resample(df)) for i in range(iters)]

Here’s how we call it. The result is a sample from the sampling distribution of differences in means.

t1 = sampling_dist(brfss, diff_means)
np.mean(t1)

14.433755828000592

The following function uses KDE to estimate the density of the sampling distribution, uses the estimated density to compute a confidence interval, and generates a plot that shows the sampling distribution, the mean, and the 95% CI.

from scipy.stats import gaussian_kde
from empiricaldist import Pmf


def plot_sampling_distribution(data, format_str=".2f", **options):
    """Plot the sampling distribution, mean and CI

    data: sample from the sampling distribution
    format_str: used to format the values
    options: passed to plt.plot
    """
    # compute the mean and CI
    m, s = np.mean(data), np.std(data)
    qs = np.linspace(m - 4 * s, m + 4 * s, 501)
    ps = gaussian_kde(data)(qs)
    pmf = Pmf(ps, qs)
    pmf.normalize()
    low, high = pmf.make_cdf().inverse([0.025, 0.975])

    # plot the density
    pmf.plot(**options)
    inside = pmf[(pmf.qs >= low) & (pmf.qs <= high)]
    plt.fill_between(inside.index, inside, color="gray", alpha=0.2)

    y = pmf.max()
    ax = plt.gca()

    # add text and lines
    plt.text(m, 0.4 * y, "mean", fontsize=14, ha="center")
    plt.text(m, 0.05 * y, f"95% CI", fontsize=14, ha="center")
    plt.plot([m, m], [0, y], ls=":", color="gray")
    plt.plot([low, high], [0, 0], ls="-", color="gray")

    # adjust xticks
    ticks = [low, m, high]
    labels = [format(tick, format_str) for tick in ticks]
    ax.tick_params(axis="x", labelsize=14)
    plt.xticks(ticks, labels)
    plt.yticks([])

    # remove spines
    for spine in ax.spines.values():
        spine.set_visible(False)

from scipy.stats import gaussian_kde
from empiricaldist import Pmf


def simple_plot(data, format_str=".2f", **options):
    """Plot the sampling distribution, mean and CI

    data: sample from the sampling distribution
    format_str: used to format the values
    options: passed to plt.plot
    """
    # compute the mean and CI
    m, s = np.mean(data), np.std(data)
    qs = np.linspace(m - 4 * s, m + 4 * s, 501)
    ps = gaussian_kde(data)(qs)
    pmf = Pmf(ps, qs)
    pmf.normalize()
    low, high = pmf.make_cdf().inverse([0.025, 0.975])

    # plot the density
    pmf.plot(**options)

    y = pmf.max()
    ax = plt.gca()

    # adjust xticks
    ticks = [low, m, high]
    labels = [format(tick, format_str) for tick in ticks]
    ax.tick_params(axis="x", labelsize=14)
    # plt.xticks(ticks, labels)
    plt.yticks([])

    # remove spines
    for spine in ax.spines.values():
        spine.set_visible(False)

Here are the results for the sampling distribution of the difference in means.

simple_plot(t1)
plt.title("Difference in means (cm)", fontsize=14)
plt.tight_layout()
plt.savefig("variability0.png", dpi=300)

plot_sampling_distribution(t1)
plt.title("Difference in means (cm)", fontsize=14)
plt.tight_layout()
plt.savefig("variability1.png", dpi=300)

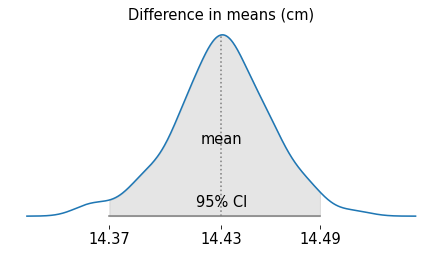
The difference in means is about 14.4 cm. If we simulate the data collection process and compute the difference in means many times, it varies a little, but it is never close to zero.

The following function estimates the probability that a value from this distribution exceeds 0, which is the p-value for the hypothesis that men are taller than women on average.

from scipy.stats import norm


def p_value(t):
    m, s = np.mean(t), np.std(t)
    if m > 0:
        return norm.cdf(0, m, s)
    else:
        return norm.sf(0, m, s)

The p-value is so close to zero we can’t compute it with floating-point arithmetic, which means it is truly negligible.

p_value(t1)

0.0

This result means that if we collect another sample this size from the same population, it is practically impossible that the women in the sample would be taller, on average.

To go a step farther, we can reasonably conclude that the difference we see in the sample is very unlikely to have occurred by chance. Some people who interpret hypothesis tests very formally don’t like that conclusion, but I stand by it.

Difference in standard deviations

OK, now let’s get serious. If men are more variable than women, we expect the standard deviation of their heights to be higher. To see if it is, all we have to do is provide a function that takes a sample and computes the difference in standard deviations.

def diff_stds(sample):
    """Difference in standard deviation (M minus female)

    sample: DataFrame with `_SEX` and `HTM4` columns

    returns: float
    """
    grouped_heights = sample.groupby("_SEX")["HTM4"]
    return -diff(grouped_heights.std())

Based on a single resampling, is looks like the standard deviation of heights is higher for men.

diff_stds(sample)

0.7755433526023632

We can use sampling_dist again with a different test statistic.

t2 = sampling_dist(brfss, diff_stds)
np.mean(t2)

0.8125943377103155

Here’s the sampling distribution with its mean and 95% CI.

plot_sampling_distribution(t2)
plt.title("Difference in standard deviation (cm)", fontsize=14)
plt.tight_layout()
plt.savefig("variability2.png", dpi=300)

The 95% CI does not contain zero, which indicates that the difference is significant at the 5% level. Assuming that the tails of the distribution drop off like the tails of a normal distribution, we can estimate the p-value like this.

p_value(t2)

3.314884452466515e-169

This p-value is just barely big enough to compute, but still so small we can conclude that the apparent difference is very unlikely to be due to chance.

However, comparing standard deviations might not be a sensible way to assess whether men are more variable. Men are taller, on average, so if their heights vary more in absolute terms, that’s doesn’t necessarily means that they vary more in relative terms. If we think that variation relative to the mean is more relevant to the variability hypothesis, another test statistic to consider is the coefficient of variation.

Difference in coefficient of variation

The coefficient of variation is the ratio of the standard deviation to the mean, so it quantifies variability in relative terms. Here’s a function that takes a sample and computes the difference in coefficients of variation for men and women.

def diff_cvs(sample):
    """Difference in CV (M minus female)

    sample: DataFrame with `_SEX` and `HTM4` columns

    returns: float
    """
    grouped_heights = sample.groupby("_SEX")["HTM4"]
    means = grouped_heights.mean()
    stds = grouped_heights.std()
    return -diff(stds / means)

And here’s a sample from the sampling distribution of the differences.

t3 = sampling_dist(brfss, diff_cvs)
np.mean(t3)

0.0006739584748971127

Here’s the sampling distribution and a 95% CI.

plot_sampling_distribution(t3, format_str="0.4f")
plt.title("Difference in coefficient of variation", fontsize=14)
plt.tight_layout()
plt.savefig("variability3.png", dpi=300)

The CI does not contain zero, so the difference is statistically significant. And the p-value is small.

p_value(t3)

4.9123330373066635e-05

But in practical terms, the difference is very small. The coefficients of variations are about 0.048.

grouped_heights = sample.groupby("_SEX")["HTM4"]
means = grouped_heights.mean()
stds = grouped_heights.std()
CVs = stds / means
CVs

_SEX
1.0    0.048558
2.0    0.048107
Name: HTM4, dtype: float64

If we express the difference in CVs and a percentage of the CVs, it is only about 1.4%.

np.mean(t3) / CVs * 100

_SEX
1.0    1.387945
2.0    1.400971
Name: HTM4, dtype: float64

By this measure of variability, men’s heights are slightly more variable than women’s, but the difference is so small, it is unlikely to have any practical consequences.

Also, both standard deviation and coefficient of variation are affected by outliers, and we have seen that there are extreme values in this dataset that are probably not correct. It’s possible that the apparent difference in variability, by these test statistics, is the result of data errors.

So let’s try again with a more robust statistic.

Difference in robust CV

As an alternative to the coefficient of variation, we can use a more robust measure of variability. One option is the ratio of the median absolute deviation (MAD) to the median. Here’s a function that computes it.

def robust_cv(series):
    """Median absolute deviation.

    series: Series of numbers

    returns: float
    """
    m = series.median()
    deviations = series - m
    return deviations.abs().median() / m

The following function computes the difference in robust CVs. The first line jitters the data – otherwise we would get the same results from every resampling.

def diff_robust_cv(sample):
    """Difference in robust CV (M minus female)

    sample: DataFrame with `_SEX` and `HTM4` columns

    returns: float
    """
    sample["HTM4"] += np.random.normal(0, 1, size=len(sample))
    grouped_heights = sample.groupby("_SEX")["HTM4"]
    rcvs = grouped_heights.apply(robust_cv)
    return -diff(rcvs)

The robust CV of the sample is negative, which suggests that women’s heights are more variable.

diff_robust_cv(sample)

-0.0025971928221166715

Here’s the sampling distribution.

t4 = sampling_dist(brfss, diff_robust_cv)
np.mean(t4)

-0.002502441445045549

plot_sampling_distribution(t4, format_str="0.4f")
plt.title("Difference in robust CV", fontsize=14)
plt.tight_layout()
plt.savefig("variability4.png", dpi=300)

And the p-value.

p_value(t4)

6.93074075784399e-122

According to the robust CV, women are more variable, but again the difference is so small it has no practical consequences.

Discussion

This example demonstrates a strength of bootstrap resampling – it is easy to explore multiple test statistics and consider which is most relevant to the hypothesis in question.

• If we compare standard deviations of height, men are more variable, but that’s not too surprising – men are taller, and almost any process that makes bigger things probably makes more variable things, too.

• Coefficient of variation might be a better way to compare things with different sizes. By that standard, men are still slightly more variable, but the difference is so small, it’s hard to imagine it has any practical consequences.

• And it might be an artifact of errors in the data. If we use a robust alternative to the coefficient of variation – MAD divided by median – women are more variable. But again, it is probably not a difference that makes a difference.

In conclusion, the distribution of human height doesn’t provide much support for the variability hypothesis.

Difference in IQR / median

Here’s one more robust measure of variability.

def diff_relative_iqr(sample):
    """Difference in IQR / median (M minus female)

    sample: DataFrame with `_SEX` and `HTM4` columns

    returns: float
    """
    sample["HTM4"] += np.random.normal(0, 1, size=len(sample))
    grouped_heights = sample.groupby("_SEX")["HTM4"]
    medians = grouped_heights.median()
    
    # the results depend on which quantiles we use
    iqrs = grouped_heights.quantile(0.75) - grouped_heights.quantile(0.25)
    #iqrs = grouped_heights.quantile(0.95) - grouped_heights.quantile(0.05)
    
    return -diff(iqrs / medians)

diff_relative_iqr(sample)

-0.0031180661772347157

t5 = sampling_dist(brfss, diff_relative_iqr)
np.mean(t5)

-0.004621824998497872

plot_sampling_distribution(t5, format_str="0.4f")
plt.title("Difference in IQR / median", fontsize=14)
plt.tight_layout()
plt.savefig("variability5.png", dpi=300)

p_value(t5)

6.773833573553618e-98