You can order print and ebook versions of Think Python 3e from Bookshop.org and Amazon.
10. Dictionaries#
This chapter presents a built-in type called a dictionary. It is one of Python’s best features – and the building block of many efficient and elegant algorithms.
We’ll use dictionaries to compute the number of unique words in a book and the number of times each one appears. And in the exercises, we’ll use dictionaries to solve word puzzles.
10.1. A dictionary is a mapping#
A dictionary is like a list, but more general. In a list, the indices have to be integers; in a dictionary they can be (almost) any type. For example, suppose we make a list of number words, like this.
lst = ['zero', 'one', 'two']
We can use an integer as an index to get the corresponding word.
lst[1]
'one'
But suppose we want to go in the other direction, and look up a word to get the corresponding integer.
We can’t do that with a list, but we can with a dictionary.
We’ll start by creating an empty dictionary and assigning it to numbers.
numbers = {}
numbers
{}
The curly braces, {}, represent an empty dictionary.
To add items to the dictionary, we’ll use square brackets.
numbers['zero'] = 0
This assignment adds to the dictionary an item, which represents the association of a key and a value.
In this example, the key is the string 'zero' and the value is the integer 0.
If we display the dictionary, we see that it contains one item, which contains a key and a value separated by a colon, :.
numbers
{'zero': 0}
We can add more items like this.
numbers['one'] = 1
numbers['two'] = 2
numbers
{'zero': 0, 'one': 1, 'two': 2}
Now the dictionary contains three items.
To look up a key and get the corresponding value, we use the bracket operator.
numbers['two']
2
If the key isn’t in the dictionary, we get a KeyError.
numbers['three']
KeyError: 'three'
The len function works on dictionaries; it returns the number of items.
len(numbers)
3
In mathematical language, a dictionary represents a mapping from keys to values, so you can also say that each key “maps to” a value. In this example, each number word maps to the corresponding integer.
The following figure shows the state diagram for numbers.
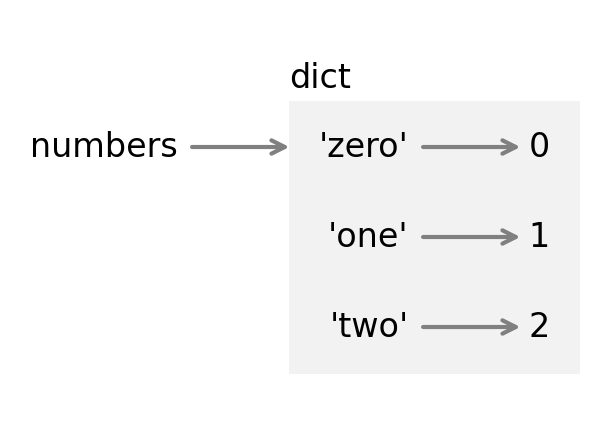
A dictionary is represented by a box with the word “dict” outside and the items inside. Each item is represented by a key and an arrow pointing to a value. The quotation marks indicate that the keys here are strings, not variable names.
10.2. Creating dictionaries#
In the previous section we created an empty dictionary and added items one at a time using the bracket operator. Instead, we could have created the dictionary all at once like this.
numbers = {'zero': 0, 'one': 1, 'two': 2}
Each item consists of a key and a value separated by a colon. The items are separated by commas and enclosed in curly braces.
Another way to create a dictionary is to use the dict function.
We can make an empty dictionary like this.
empty = dict()
empty
{}
And we can make a copy of a dictionary like this.
numbers_copy = dict(numbers)
numbers_copy
{'zero': 0, 'one': 1, 'two': 2}
It is often useful to make a copy before performing operations that modify dictionaries.
10.3. The in operator#
The in operator works on dictionaries, too; it tells you whether something appears as a key in the dictionary.
'one' in numbers
True
The in operator does not check whether something appears as a value.
1 in numbers
False
To see whether something appears as a value in a dictionary, you can use the method values, which returns a sequence of values, and then use the in operator.
1 in numbers.values()
True
The items in a Python dictionary are stored in a hash table, which is a way of organizing data that has a remarkable property: the in operator takes about the same amount of time no matter how many items are in the dictionary.
That makes it possible to write some remarkably efficient algorithms.
To demonstrate, we’ll compare two algorithms for finding pairs of words where one is the reverse of another – like stressed and desserts.
We’ll start by reading the word list.
word_list = open('words.txt').read().split()
len(word_list)
113783
And here’s reverse_word from the previous chapter.
def reverse_word(word):
return ''.join(reversed(word))
The following function loops through the words in the list. For each one, it reverses the letters and then checks whether the reversed word is in the word list.
def too_slow():
count = 0
for word in word_list:
if reverse_word(word) in word_list:
count += 1
return count
This function takes more than a minute to run.
The problem is that the in operator checks the words in the list one at a time, starting at the beginning.
If it doesn’t find what it’s looking for – which happens most of the time – it has to search all the way to the end.
And the in operator is inside the loop, so it runs once for each word.
Since there are more than 100,000 words in the list, and for each one we check more than 100,000 words, the total number of comparisons is the number of words squared – roughly – which is almost 13 billion.
len(word_list)**2
12946571089
We can make this function much faster with a dictionary. The following loop creates a dictionary that contains the words as keys.
word_dict = {}
for word in word_list:
word_dict[word] = 1
The values in word_dict are all 1, but they could be anything, because we won’t ever look them up – we will only use this dictionary to check whether a key exists.
Now here’s a version of the previous function that replaces word_list with word_dict.
def much_faster():
count = 0
for word in word_dict:
if reverse_word(word) in word_dict:
count += 1
return count
This function takes less than one hundredth of a second, so it’s about 10,000 times faster than the previous version.
In general, the time it takes to find an element in a list is proportional to the length of the list. The time it takes to find a key in a dictionary is almost constant – regardless of the number of items.
10.4. A collection of counters#
Suppose you are given a string and you want to count how many times each letter appears. A dictionary is a good tool for this job. We’ll start with an empty dictionary.
counter = {}
As we loop through the letters in the string, suppose we see the letter 'a' for the first time.
We can add it to the dictionary like this.
counter['a'] = 1
The value 1 indicates that we have seen the letter once.
Later, if we see the same letter again, we can increment the counter like this.
counter['a'] += 1
Now the value associated with 'a' is 2, because we’ve seen the letter twice.
counter
{'a': 2}
The following function uses these features to count the number of times each letter appears in a string.
def value_counts(string):
counter = {}
for letter in string:
if letter not in counter:
counter[letter] = 1
else:
counter[letter] += 1
return counter
Each time through the loop, if letter is not in the dictionary, we create a new item with key letter and value 1.
If letter is already in the dictionary we increment the value associated with letter.
Here’s an example.
counter = value_counts('brontosaurus')
counter
{'b': 1, 'r': 2, 'o': 2, 'n': 1, 't': 1, 's': 2, 'a': 1, 'u': 2}
The items in counter show that the letter 'b' appears once, 'r' appears twice, and so on.
10.5. Looping and dictionaries#
If you use a dictionary in a for statement, it traverses the keys of the dictionary.
To demonstrate, let’s make a dictionary that counts the letters in 'banana'.
counter = value_counts('banana')
counter
{'b': 1, 'a': 3, 'n': 2}
The following loop prints the keys, which are the letters.
for key in counter:
print(key)
b
a
n
To print the values, we can use the values method.
for value in counter.values():
print(value)
1
3
2
To print the keys and values, we can loop through the keys and look up the corresponding values.
for key in counter:
value = counter[key]
print(key, value)
b 1
a 3
n 2
In the next chapter, we’ll see a more concise way to do the same thing.
10.6. Lists and dictionaries#
You can put a list in a dictionary as a value.
For example, here’s a dictionary that maps from the number 4 to a list of four letters.
d = {4: ['r', 'o', 'u', 's']}
d
{4: ['r', 'o', 'u', 's']}
But you can’t put a list in a dictionary as a key. Here’s what happens if we try.
letters = list('abcd')
d[letters] = 4
TypeError: unhashable type: 'list'
I mentioned earlier that dictionaries use hash tables, and that means that the keys have to be hashable.
A hash is a function that takes a value (of any kind) and returns an integer. Dictionaries use these integers, called hash values, to store and look up keys.
This system only works if a key is immutable, so its hash value is always the same. But if a key is mutable, its hash value could change, and the dictionary would not work. That’s why keys have to be hashable, and why mutable types like lists aren’t.
Since dictionaries are mutable, they can’t be used as keys, either. But they can be used as values.
10.7. Accumulating a list#
For many programming tasks, it is useful to loop through one list or dictionary while building another.
As an example, we’ll loop through the words in word_dict and make a list of palindromes – that is, words that are spelled the same backward and forward, like “noon” and “rotator”.
In the previous chapter, one of the exercises asked you to write a function that checks whether a word is a palindrome.
Here’s a solution that uses reverse_word.
def is_palindrome(word):
"""Check if a word is a palindrome."""
return reverse_word(word) == word
If we loop through the words in word_dict, we can count the number of palindromes like this.
count = 0
for word in word_dict:
if is_palindrome(word):
count +=1
count
91
By now, this pattern is familiar.
Before the loop,
countis initialized to0.Inside the loop, if
wordis a palindrome, we incrementcount.When the loop ends,
countcontains the total number of palindromes.
We can use a similar pattern to make a list of palindromes.
palindromes = []
for word in word_dict:
if is_palindrome(word):
palindromes.append(word)
palindromes[:10]
['aa', 'aba', 'aga', 'aha', 'ala', 'alula', 'ama', 'ana', 'anna', 'ava']
Here’s how it works:
Before the loop,
palindromesis initialized with an empty list.Inside the loop, if
wordis a palindrome, we append it to the end ofpalindromes.When the loop ends,
palindromesis a list of palindromes.
In this loop, palindromes is used as an accumulator, which is a variable that collects or accumulates data during a computation.
Now suppose we want to select only palindromes with seven or more letters.
We can loop through palindromes and make a new list that contains only long palindromes.
long_palindromes = []
for word in palindromes:
if len(word) >= 7:
long_palindromes.append(word)
long_palindromes
['deified', 'halalah', 'reifier', 'repaper', 'reviver', 'rotator', 'sememes']
Looping through a list like this, selecting some elements and omitting others, is called filtering.
10.8. Memos#
If you ran the fibonacci function from Chapter 6, maybe you noticed that the bigger the argument you provide, the longer the function takes to run.
def fibonacci(n):
if n == 0:
return 0
if n == 1:
return 1
return fibonacci(n-1) + fibonacci(n-2)
Furthermore, the run time increases quickly.
To understand why, consider the following figure, which shows the call graph for
fibonacci with n=4:
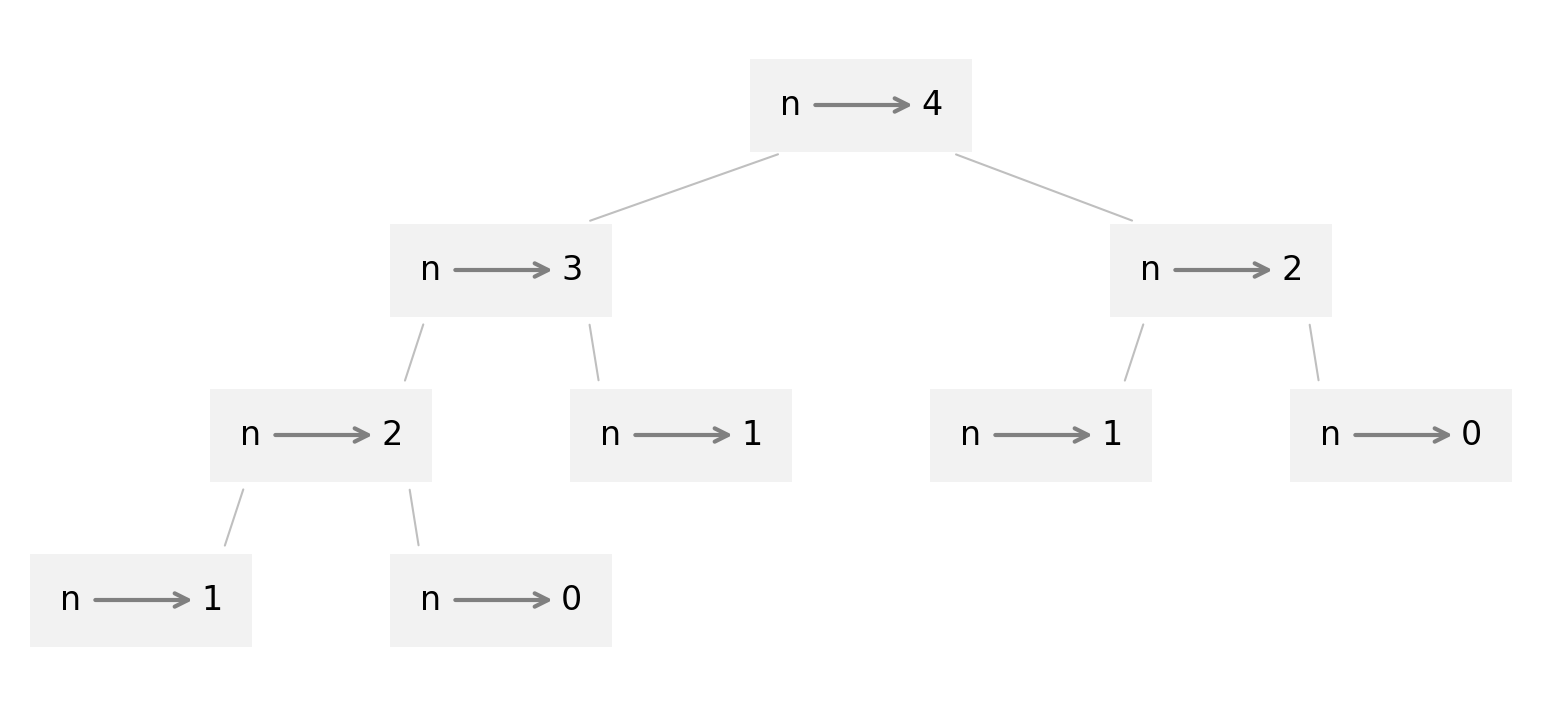
A call graph shows a set of function frames, with lines connecting each frame to the frames of the functions it calls.
At the top of the graph, fibonacci with n=4 calls fibonacci with n=3 and n=2.
In turn, fibonacci with n=3 calls fibonacci with n=2 and n=1. And so on.
Count how many times fibonacci(0) and fibonacci(1) are called.
This is an inefficient solution to the problem, and it gets worse as the argument gets bigger.
One solution is to keep track of values that have already been computed by storing them in a dictionary.
A previously computed value that is stored for later use is called a memo.
Here is a “memoized” version of fibonacci:
known = {0:0, 1:1}
def fibonacci_memo(n):
if n in known:
return known[n]
res = fibonacci_memo(n-1) + fibonacci_memo(n-2)
known[n] = res
return res
known is a dictionary that keeps track of the Fibonacci numbers we already know
It starts with two items: 0 maps to 0 and 1 maps to 1.
Whenever fibonacci_memo is called, it checks known.
If the result is already there, it can return immediately.
Otherwise it has to compute the new value, add it to the dictionary, and return it.
Comparing the two functions, fibonacci(40) takes about 30 seconds to run.
fibonacci_memo(40) takes about 30 microseconds, so it’s a million times faster.
In the notebook for this chapter, you’ll see where these measurements come from.
10.9. Debugging#
As you work with bigger datasets it can become unwieldy to debug by printing and checking the output by hand. Here are some suggestions for debugging large datasets:
Scale down the input: If possible, reduce the size of the dataset. For example if the program reads a text file, start with just the first 10 lines, or with the smallest example you can find. You can either edit the files themselves, or (better) modify the program so it reads only the first
nlines.If there is an error, you can reduce
nto the smallest value where the error occurs. As you find and correct errors, you can increasengradually.
Check summaries and types: Instead of printing and checking the entire dataset, consider printing summaries of the data – for example, the number of items in a dictionary or the total of a list of numbers.
A common cause of runtime errors is a value that is not the right type. For debugging this kind of error, it is often enough to print the type of a value.
Write self-checks: Sometimes you can write code to check for errors automatically. For example, if you are computing the average of a list of numbers, you could check that the result is not greater than the largest element in the list or less than the smallest. This is called a “sanity check” because it detects results that are “insane”.
Another kind of check compares the results of two different computations to see if they are consistent. This is called a “consistency check”.
Format the output: Formatting debugging output can make it easier to spot an error. We saw an example in Chapter 6. Another tool you might find useful is the
pprintmodule, which provides apprintfunction that displays built-in types in a more human-readable format (pprintstands for “pretty print”).Again, time you spend building scaffolding can reduce the time you spend debugging.
10.10. Glossary#
dictionary: An object that contains key-value pairs, also called items.
item: In a dictionary, another name for a key-value pair.
key: An object that appears in a dictionary as the first part of a key-value pair.
value: An object that appears in a dictionary as the second part of a key-value pair. This is more specific than our previous use of the word “value”.
mapping: A relationship in which each element of one set corresponds to an element of another set.
hash table: A collection of key-value pairs organized so that we can look up a key and find its value efficiently.
hashable: Immutable types like integers, floats and strings are hashable. Mutable types like lists and dictionaries are not.
hash function: A function that takes an object and computes an integer that is used to locate a key in a hash table.
accumulator: A variable used in a loop to add up or accumulate a result.
filtering: Looping through a sequence and selecting or omitting elements.
call graph: A diagram that shows every frame created during the execution of a program, with an arrow from each caller to each callee.
memo: A computed value stored to avoid unnecessary future computation.
10.11. Exercises#
# This cell tells Jupyter to provide detailed debugging information
# when a runtime error occurs. Run it before working on the exercises.
%xmode Verbose
10.11.1. Ask a virtual assistant#
In this chapter, I said the keys in a dictionary have to be hashable and I gave a short explanation. If you would like more details, ask a virtual assistant, “Why do keys in Python dictionaries have to be hashable?”
In a previous section, we stored a list of words as keys in a dictionary so that we could use an efficient version of the in operator.
We could have done the same thing using a set, which is another built-in data type.
Ask a virtual assistant, “How do I make a Python set from a list of strings and check whether a string is an element of the set?”
10.11.2. Exercise#
Dictionaries have a method called get that takes a key and a default value.
If the key appears in the dictionary, get returns the corresponding value; otherwise it returns the default value.
For example, here’s a dictionary that maps from the letters in a string to the number of times they appear.
counter = value_counts('brontosaurus')
If we look up a letter that appears in the word, get returns the number of times it appears.
counter.get('b', 0)
1
If we look up a letter that doesn’t appear, we get the default value, 0.
counter.get('c', 0)
0
Use get to write a more concise version of value_counts.
You should be able to eliminate the if statement.
10.11.3. Exercise#
What is the longest word you can think of where each letter appears only once?
Let’s see if we can find one longer than unpredictably.
Write a function named has_duplicates that takes a sequence – like a list or string – as a parameter and returns True if there is any element that appears in the sequence more than once.
10.11.4. Exercise#
Write a function called find_repeats that takes a dictionary that maps from each key to a counter, like the result from value_counts.
It should loop through the dictionary and return a list of keys that have counts greater than 1.
You can use the following outline to get started.
def find_repeats(counter):
"""Makes a list of keys with values greater than 1.
counter: dictionary that maps from keys to counts
returns: list of keys
"""
return []
10.11.5. Exercise#
Suppose you run value_counts with two different words and save the results in two dictionaries.
counter1 = value_counts('brontosaurus')
counter2 = value_counts('apatosaurus')
Each dictionary maps from a set of letters to the number of times they appear.
Write a function called add_counters that takes two dictionaries like this and returns a new dictionary that contains all of the letters and the total number of times they appear in either word.
There are many ways to solve this problem. Once you have a working solution, consider asking a virtual assistant for different solutions.
10.11.6. Exercise#
A word is “interlocking” if we can split it into two words by taking alternating letters. For example, “schooled” is an interlocking word because it can be split into “shoe” and “cold”.
To select alternating letters from a string, you can use a slice operator with three components that indicate where to start, where to stop, and the “step size” between the letters.
In the following slice, the first component is 0, so we start with the first letter.
The second component is None, which means we should go all the way to the end of the string.
And the third component is 2, so there are two steps between the letters we select.
word = 'schooled'
first = word[0:None:2]
first
'shoe'
Instead of providing None as the second component, we can get the same effect by leaving it out altogether.
For example, the following slice selects alternating letters, starting with the second letter.
second = word[1::2]
second
'cold'
Write a function called is_interlocking that takes a word as an argument and returns True if it can be split into two interlocking words.
for word in word_list:
if len(word) >= 8 and is_interlocking(word):
first = word[0::2]
second = word[1::2]
print(word, first, second)
Copyright 2024 Allen B. Downey
Code license: MIT License
Text license: Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International