Variables and Statements#
In the previous chapter, we used operators to write expressions that perform arithmetic computations.
In this chapter, you’ll learn about variables and statements, the import statement, and the print function.
And I’ll introduce more of the vocabulary we use to talk about programs, including “argument” and “module”.
Variables#
A variable is a name that refers to a value. To create a variable, we can write a assignment statement like this.
n = 17
An assignment statement has three parts: the name of the variable on the left, the equals operator, =, and an expression on the right.
In this example, the expression is an integer.
In the following example, the expression is a floating-point number.
pi = 3.141592653589793
And in the following example, the expression is a string.
message = 'And now for something completely different'
When you run an assignment statement, there is no output.
Python creates the variable and gives it a value, but the assignment statement has no visible effect.
However, after creating a variable, you can use it as an expression.
So we can display the value of message like this:
message
'And now for something completely different'
You can also use a variable as part of an expression with arithmetic operators.
n + 25
42
2 * pi
6.283185307179586
And you can use a variable when you call a function.
round(pi)
3
len(message)
42
State diagrams#
A common way to represent variables on paper is to write the name with an arrow pointing to its value.
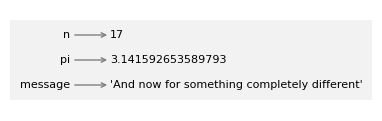
This kind of figure is called a state diagram because it shows what state each of the variables is in (think of it as the variable’s state of mind). We’ll use state diagrams throughout the book to represent a model of how Python stores variables and their values.
Variable names#
Variable names can be as long as you like. They can contain both letters and numbers, but they can’t begin with a number. It is legal to use uppercase letters, but it is conventional to use only lower case for variable names.
The only punctuation that can appear in a variable name is the underscore character, _. It is often used in names with multiple words, such as your_name or airspeed_of_unladen_swallow.
If you give a variable an illegal name, you get a syntax error.
The name million! is illegal because it contains punctuation.
million! = 1000000
Cell In[12], line 1
million! = 1000000
^
SyntaxError: invalid syntax
76trombones is illegal because it starts with a number.
76trombones = 'big parade'
Cell In[13], line 1
76trombones = 'big parade'
^
SyntaxError: invalid decimal literal
class is also illegal, but it might not be obvious why.
class = 'Self-Defence Against Fresh Fruit'
Cell In[14], line 1
class = 'Self-Defence Against Fresh Fruit'
^
SyntaxError: invalid syntax
It turns out that class is a keyword, which is a special word used to specify the structure of a program.
Keywords can’t be used as variable names.
Here’s a complete list of Python’s keywords:
False await else import pass
None break except in raise
True class finally is return
and continue for lambda try
as def from nonlocal while
assert del global not with
async elif if or yield
You don’t have to memorize this list. In most development environments, keywords are displayed in a different color; if you try to use one as a variable name, you’ll know.
The import statement#
In order to use some Python features, you have to import them.
For example, the following statement imports the math module.
import math
A module is a collection of variables and functions.
The math module provides a variable called pi that contains the value of the mathematical constant denoted \(\pi\).
We can display its value like this.
math.pi
3.141592653589793
To use a variable in a module, you have to use the dot operator (.) between the name of the module and the name of the variable.
The math module also contains functions.
For example, sqrt computes square roots.
math.sqrt(25)
5.0
And pow raises one number to the power of a second number.
math.pow(5, 2)
25.0
At this point we’ve seen two ways to raise a number to a power: we can use the math.pow function or the exponentiation operator, **.
Either one is fine, but the operator is used more often than the function.
Expressions and statements#
So far, we’ve seen a few kinds of expressions. An expression can be a single value, like an integer, floating-point number, or string. It can also be a collection of values and operators. And it can include variable names and function calls. Here’s an expression that includes several of these elements.
19 + n + round(math.pi) * 2
42
We have also seen a few kind of statements. A statement is a unit of code that has an effect, but no value. For example, an assignment statement creates a variable and gives it a value, but the statement itself has no value.
n = 17
Similarly, an import statement has an effect – it imports a module so we can use the values and functions it contains – but it has no visible effect.
import math
Computing the value of an expression is called evaluation. Running a statement is called execution.
The print function#
When you evaluate an expression, the result is displayed.
n + 1
18
But if you evaluate more than one expression, only the value of the last one is displayed.
n + 2
n + 3
20
To display more than one value, you can use the print function.
print(n+2)
print(n+3)
19
20
It also works with floating-point numbers and strings.
print('The value of pi is approximately')
print(math.pi)
The value of pi is approximately
3.141592653589793
You can also use a sequence of expressions separated by commas.
print('The value of pi is approximately', math.pi)
The value of pi is approximately 3.141592653589793
Notice that the print function puts a space between the values.
Arguments#
When you call a function, the expression in parenthesis is called an argument. Normally I would explain why, but in this case the technical meaning of a term has almost nothing to do with the common meaning of the word, so I won’t even try.
Some of the functions we’ve seen so far take only one argument, like int.
int('101')
101
Some take two, like math.pow.
math.pow(5, 2)
25.0
Some can take additional arguments that are optional.
For example, int can take a second argument that specifies the base of the number.
int('101', 2)
5
The sequence of digits 101 in base 2 represents the number 5 in base 10.
round also takes an optional second argument, which is the number of decimal places to round off to.
round(math.pi, 3)
3.142
Some functions can take any number of arguments, like print.
print('Any', 'number', 'of', 'arguments')
Any number of arguments
If you call a function and provide too many arguments, that’s a TypeError.
float('123.0', 2)
TypeError: float expected at most 1 argument, got 2
If you provide too few arguments, that’s also a TypeError.
math.pow(2)
TypeError: pow expected 2 arguments, got 1
And if you provide an argument with a type the function can’t handle, that’s a TypeError, too.
math.sqrt('123')
TypeError: must be real number, not str
This kind of checking can be annoying when you are getting started, but it helps you detect and correct errors.
Debugging#
Three kinds of errors can occur in a program: syntax errors, runtime errors, and semantic errors. It is useful to distinguish between them in order to track them down more quickly.
Syntax error: “Syntax” refers to the structure of a program and the rules about that structure. If there is a syntax error anywhere in your program, Python does not run the program. It displays an error message immediately.
Runtime error: If there are no syntax errors in your program, it can start running. But if something goes wrong, Python displays an error message and stops. This type of error is called a runtime error. It is also called an exception because it indicates that something exceptional has happened.
Semantic error: The third type of error is “semantic”, which means related to meaning. If there is a semantic error in your program, it runs without generating error messages, but it does not do what you intended. Identifying semantic errors can be tricky because it requires you to work backward by looking at the output of the program and trying to figure out what it is doing.
As we’ve seen, an illegal variable name is a syntax error.
million! = 1000000
Cell In[40], line 1
million! = 1000000
^
SyntaxError: invalid syntax
If you use an operator with a type it doesn’t support, that’s a runtime error.
'126' / 3
TypeError: unsupported operand type(s) for /: 'str' and 'int'
Finally, here’s an example of a semantic error.
Suppose we want to compute the average of 1 and 3, but we forget about the order of operations and write this:
1 + 3 / 2
2.5
When this expression is evaluated, it does not produce an error message, so there is no syntax error or runtime error.
But the result is not the average of 1 and 3, so the program is not correct.
This is a semantic error because the program runs but it doesn’t do what’s intended.
Glossary#
variable: A name that refers to a value.
assignment statement: A statement that assigns a value to a variable.
state diagram: A graphical representation of a set of variables and the values they refer to.
keyword: A special word used to specify the structure of a program.
import statement: A statement that reads a module file and creates a module object.
module: A file that contains Python code, including function definitions and sometimes other statements.
dot operator:
The operator, ., used to access a function in another module by specifying the module name followed by a dot and the function name.
evaluate: Perform the operations in an expression in order to compute a value.
statement: One or more lines of code that represent a command or action.
execute: Run a statement and do what it says.
argument: A value provided to a function when the function is called. Each argument is assigned to the corresponding parameter in the function.
comment: Text included in a program that provides information about the program but has no effect on its execution.
runtime error: An error that causes a program to display an error message and exit.
exception: An error that is detected while the program is running.
semantic error: An error that causes a program to do the wrong thing, but not to display an error message.
Exercises#
# This cell tells Jupyter to provide detailed debugging information
# when a runtime error occurs. Run it before working on the exercises.
%xmode Verbose
Ask a virtual assistant#
Again, I encourage you to use a virtual assistant to learn more about any of the topics in this chapter.
If you are curious about any of keywords I listed, you could ask “Why is class a keyword?” or “Why can’t variable names be keywords?”
You might have noticed that int, float, and str are not Python keywords.
They are variables that represent types, and they can be used as functions.
So it is legal to have a variable or function with one of those names, but it is strongly discouraged. Ask an assistant “Why is it bad to use int, float, and string as variable names?”
Also ask, “What are the built-in functions in Python?” If you are curious about any of them, ask for more information.
In this chapter we imported the math module and used some of the variable and functions it provides. Ask an assistant, “What variables and functions are in the math module?” and “Other than math, what modules are in considered core Python?”
Exercise#
Repeating my advice from the previous chapter, whenever you learn a new feature, you should make errors on purpose to see what goes wrong.
We’ve seen that
n = 17is legal. What about17 = n?How about
x = y = 1?In some languages every statement ends with a semi-colon (
;). What happens if you put a semi-colon at the end of a Python statement?What if you put a period at the end of a statement?
What happens if you spell the name of a module wrong and try to import
maath?
Exercise#
Practice using the Python interpreter as a calculator:
Part 1. The volume of a sphere with radius \(r\) is \(\frac{4}{3} \pi r^3\).
What is the volume of a sphere with radius 5? Start with a variable named radius and then assign the result to a variable named volume. Display the result. Add comments to indicate that radius is in centimeters and volume in cubic centimeters.
Part 2. A rule of trigonometry says that for any value of \(x\), \((\cos x)^2 + (\sin x)^2 = 1\). Let’s see if it’s true for a specific value of \(x\) like 42.
Create a variable named x with this value.
Then use math.cos and math.sin to compute the sine and cosine of \(x\), and the sum of their squared.
The result should be close to 1. It might not be exactly 1 because floating-point arithmetic is not exact—it is only approximately correct.
Part 3. In addition to pi, the other variable defined in the math module is e, which represents the base of the natural logarithm, written in math notation as \(e\). If you are not familiar with this value, ask a virtual assistant “What is math.e?” Now let’s compute \(e^2\) three ways:
Use
math.eand the exponentiation operator (**).Use
math.powto raisemath.eto the power2.Use
math.exp, which takes as an argument a value, \(x\), and computes \(e^x\).
You might notice that the last result is slightly different from the other two. See if you can find out which is correct.
Comments#
As programs get bigger and more complicated, they get more difficult to read. Formal languages are dense, and it is often difficult to look at a piece of code and figure out what it is doing and why.
For this reason, it is a good idea to add notes to your programs to explain in natural language what the program is doing. These notes are called comments, and they start with the
#symbol.In this case, the comment appears on a line by itself. You can also put comments at the end of a line:
Everything from the
#to the end of the line is ignored—it has no effect on the execution of the program.Comments are most useful when they document non-obvious features of the code. It is reasonable to assume that the reader can figure out what the code does; it is more useful to explain why.
This comment is redundant with the code and useless:
This comment contains useful information that is not in the code:
Good variable names can reduce the need for comments, but long names can make complex expressions hard to read, so there is a tradeoff.