Implementing PMFs#
This notebook outlines the API for Pmf objects in the empiricaldist library, showing the implementations of many methods.
Click here to run this notebook on Colab.
try:
import empiricaldist
except ImportError:
!pip install empiricaldist
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import inspect
def psource(obj):
"""Prints the source code for a given object.
obj: function or method object
"""
print(inspect.getsource(obj))
Constructor#
For comments or questions about this section, see this issue.
The Pmf class inherits its constructor from pd.Series.
You can create an empty Pmf and then add elements.
Here’s a Pmf that represents a six-sided die.
from empiricaldist import Pmf
d6 = Pmf()
for x in [1,2,3,4,5,6]:
d6[x] = 1
Initially the probabilities don’t add up to 1.
d6
| probs | |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1 |
| 6 | 1 |
normalize adds up the probabilities and divides through. The return value is the total probability before normalizing.
psource(Pmf.normalize)
def normalize(self):
"""Make the probabilities add up to 1 (modifies self).
Returns: normalizing constant
"""
total = self.sum()
self /= total
return total
d6.normalize()
6
Now the Pmf is normalized.
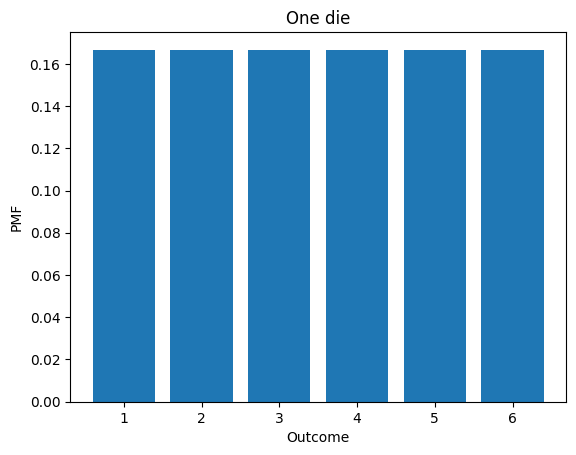
d6
| probs | |
|---|---|
| 1 | 0.166667 |
| 2 | 0.166667 |
| 3 | 0.166667 |
| 4 | 0.166667 |
| 5 | 0.166667 |
| 6 | 0.166667 |
###Properties
For comments or questions about this section, see this issue.
In a Pmf the index contains the quantities (qs) and the values contain the probabilities (ps).
These attributes are available as properties that return arrays (same semantics as the Pandas values property)
d6.qs
array([1, 2, 3, 4, 5, 6])
d6.ps
array([0.16666667, 0.16666667, 0.16666667, 0.16666667, 0.16666667,
0.16666667])
Displaying PMFs#
For comments or questions about this section, see this issue.
Pmf provides _repr_html_, so it looks good when displayed in a notebook.
psource(Pmf._repr_html_)
def _repr_html_(self):
"""Returns an HTML representation of the series.
Mostly used for Jupyter notebooks.
"""
df = pd.DataFrame(dict(probs=self))
return df._repr_html_()
Pmf provides bar, which plots the Pmf as a bar chart.
psource(Pmf.bar)
def bar(self, **options):
"""Make a bar plot.
Note: A previous version of this function used pd.Series.plot.bar,
but that was a mistake, because that function treats the quantities
as categorical, even if they are numerical, leading to hilariously
unexpected results!
Args:
options: passed to plt.bar
"""
underride(options, label=self.name)
plt.bar(self.qs, self.ps, **options)
def decorate_dice(title):
"""Labels the axes.
title: string
"""
plt.xlabel('Outcome')
plt.ylabel('PMF')
plt.title(title)
d6.bar()
decorate_dice('One die')
Pmf inherits plot from Series.
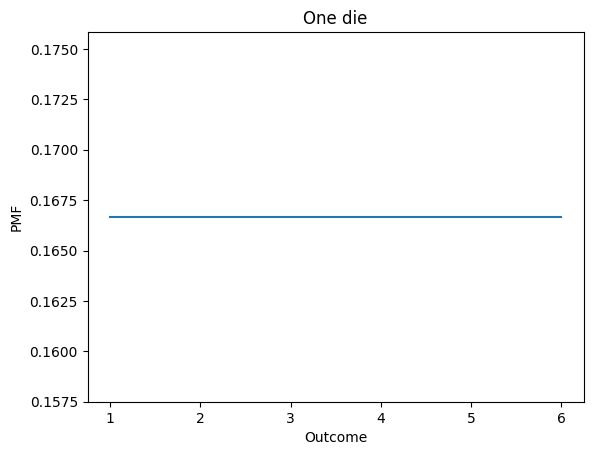
d6.plot()
decorate_dice('One die')
Make Pmf from sequence#
For comments or questions about this section, see this issue.
The following function makes a Pmf object from a sequence of values.
psource(Pmf.from_seq)
@staticmethod
def from_seq(
seq,
normalize=True,
sort=True,
ascending=True,
dropna=True,
na_position="last",
**options,
):
"""Make a PMF from a sequence of values.
Args:
seq: iterable
normalize: whether to normalize the Pmf, default True
sort: whether to sort the Pmf by values, default True
ascending: whether to sort in ascending order, default True
dropna: whether to drop NaN values, default True
na_position: If ‘first’ puts NaNs at the beginning,
‘last’ puts NaNs at the end.
options: passed to the pd.Series constructor
Returns: Pmf object
"""
# compute the value counts
series = pd.Series(seq).value_counts(
normalize=normalize, sort=False, dropna=dropna
)
# make the result a Pmf
# (since we just made a fresh Series, there is no reason to copy it)
options["copy"] = False
underride(options, name="")
pmf = Pmf(series, **options)
# sort in place, if desired
if sort:
pmf.sort_index(
inplace=True, ascending=ascending, na_position=na_position
)
return pmf
pmf = Pmf.from_seq(list('allen'))
pmf
| probs | |
|---|---|
| a | 0.2 |
| e | 0.2 |
| l | 0.4 |
| n | 0.2 |
pmf = Pmf.from_seq(np.array([1, 2, 2, 3, 5]))
pmf
| probs | |
|---|---|
| 1 | 0.2 |
| 2 | 0.4 |
| 3 | 0.2 |
| 5 | 0.2 |
Selection#
For comments or questions about this section, see this issue.
Pmf overrides __getitem__ to return 0 for values that are not in the distribution.
psource(Pmf.__getitem__)
def __getitem__(self, key):
check_dict_or_set_indexers(key)
key = com.apply_if_callable(key, self)
if key is Ellipsis:
return self
key_is_scalar = is_scalar(key)
if isinstance(key, (list, tuple)):
key = unpack_1tuple(key)
if is_integer(key) and self.index._should_fallback_to_positional:
warnings.warn(
# GH#50617
"Series.__getitem__ treating keys as positions is deprecated. "
"In a future version, integer keys will always be treated "
"as labels (consistent with DataFrame behavior). To access "
"a value by position, use `ser.iloc[pos]`",
FutureWarning,
stacklevel=find_stack_level(),
)
return self._values[key]
elif key_is_scalar:
return self._get_value(key)
# Convert generator to list before going through hashable part
# (We will iterate through the generator there to check for slices)
if is_iterator(key):
key = list(key)
if is_hashable(key) and not isinstance(key, slice):
# Otherwise index.get_value will raise InvalidIndexError
try:
# For labels that don't resolve as scalars like tuples and frozensets
result = self._get_value(key)
return result
except (KeyError, TypeError, InvalidIndexError):
# InvalidIndexError for e.g. generator
# see test_series_getitem_corner_generator
if isinstance(key, tuple) and isinstance(self.index, MultiIndex):
# We still have the corner case where a tuple is a key
# in the first level of our MultiIndex
return self._get_values_tuple(key)
if isinstance(key, slice):
# Do slice check before somewhat-costly is_bool_indexer
return self._getitem_slice(key)
if com.is_bool_indexer(key):
key = check_bool_indexer(self.index, key)
key = np.asarray(key, dtype=bool)
return self._get_rows_with_mask(key)
return self._get_with(key)
d6[1]
0.16666666666666666
d6[6]
0.16666666666666666
If you use square brackets to look up a quantity that’s not in the Pmf, you get a KeyError.
# d6[7]
Pmf objects are mutable, but in general the result is not normalized.
d7 = d6.copy()
d7[7] = 1/6
d7
| probs | |
|---|---|
| 1 | 0.166667 |
| 2 | 0.166667 |
| 3 | 0.166667 |
| 4 | 0.166667 |
| 5 | 0.166667 |
| 6 | 0.166667 |
| 7 | 0.166667 |
d7.sum()
1.1666666666666665
d7.normalize()
1.1666666666666665
d7.sum()
1.0000000000000002
Statistics#
For comments or questions about this section, see this issue.
Pmf overrides the statistics methods to compute mean, median, etc.
These functions only work correctly if the Pmf is normalized.
psource(Pmf.mean)
def mean(self):
"""Computes expected value.
Returns: float
"""
if not np.allclose(1, self.sum()):
raise ValueError("Pmf must be normalized before computing mean")
if not pd.api.types.is_numeric_dtype(self.dtype):
raise ValueError("mean is only defined for numeric data")
return np.sum(self.ps * self.qs)
d6.mean()
3.5
psource(Pmf.var)
def var(self):
"""Variance of a PMF.
Returns: float
"""
m = self.mean()
d = self.qs - m
return np.sum(d**2 * self.ps)
d6.var()
2.9166666666666665
psource(Pmf.std)
def std(self):
"""Standard deviation of a PMF.
Returns: float
"""
return np.sqrt(self.var())
d6.std()
1.707825127659933
Sampling#
For comments or questions about this section, see this issue.
choice chooses a random values from the Pmf, following the API of np.random.choice
psource(Pmf.choice)
def choice(self, *args, **kwargs):
"""Makes a random sample.
Uses the probabilities as weights unless `p` is provided.
Args:
args: same as np.random.choice
kwargs: same as np.random.choice
Returns: NumPy array
"""
underride(kwargs, p=self.ps)
return np.random.choice(self.qs, *args, **kwargs)
d6.choice(size=10)
array([3, 3, 5, 6, 1, 5, 3, 6, 6, 1])
sample chooses a random values from the Pmf, following the API of pd.Series.sample
psource(Pmf.sample)
def sample(self, *args, **kwargs):
"""Samples with replacement using probabilities as weights.
Uses the inverse CDF.
Args:
n: number of values
Returns: NumPy array
"""
cdf = self.make_cdf()
return cdf.sample(*args, **kwargs)
d6.sample(n=10)
array([3., 3., 5., 1., 1., 1., 3., 5., 3., 6.])
Arithmetic#
For comments or questions about this section, see this issue.
Pmf provides add_dist, which computes the distribution of the sum.
The implementation uses outer products to compute the convolution of the two distributions.
psource(Pmf.add_dist)
def add_dist(self, x):
"""Computes the Pmf of the sum of values drawn from self and x.
Args:
x: Distribution, scalar, or sequence
Returns: new Pmf
"""
if isinstance(x, Distribution):
return self.convolve_dist(x, np.add.outer)
else:
return Pmf(self.ps.copy(), index=self.qs + x)
psource(Pmf.convolve_dist)
def convolve_dist(self, dist, ufunc):
"""Convolve two distributions.
Args:
dist: Distribution
ufunc: elementwise function for arrays
Returns: new Pmf
"""
dist = dist.make_pmf()
qs = ufunc(self.qs, dist.qs).flatten()
ps = np.multiply.outer(self.ps, dist.ps).flatten()
series = pd.Series(ps).groupby(qs).sum()
return Pmf(series)
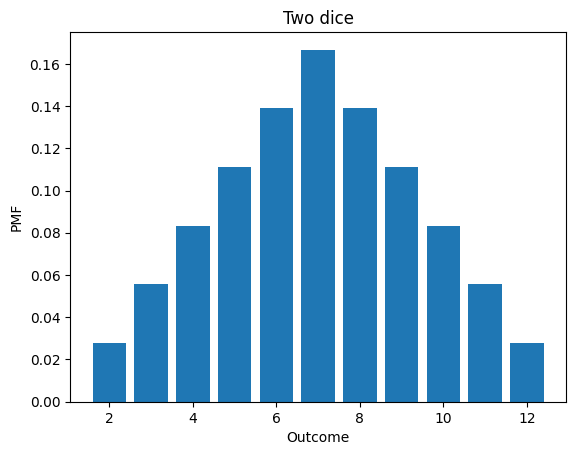
Here’s the distribution of the sum of two dice.
d6 = Pmf.from_seq([1,2,3,4,5,6])
twice = d6.add_dist(d6)
twice
| probs | |
|---|---|
| 2 | 0.027778 |
| 3 | 0.055556 |
| 4 | 0.083333 |
| 5 | 0.111111 |
| 6 | 0.138889 |
| 7 | 0.166667 |
| 8 | 0.138889 |
| 9 | 0.111111 |
| 10 | 0.083333 |
| 11 | 0.055556 |
| 12 | 0.027778 |
twice.bar()
decorate_dice('Two dice')
twice.mean()
6.999999999999998
To add a constant to a distribution, you could construct a deterministic Pmf
const = Pmf.from_seq([1])
d4.add_dist(const)
| probs | |
|---|---|
| 2 | 0.25 |
| 3 | 0.25 |
| 4 | 0.25 |
| 5 | 0.25 |
But add_dist also handles constants as a special case:
d4.add_dist(1)
| probs | |
|---|---|
| 2 | 0.25 |
| 3 | 0.25 |
| 4 | 0.25 |
| 5 | 0.25 |
Other arithmetic operations are also implemented
d6.sub_dist(d4)
| probs | |
|---|---|
| -3 | 0.041667 |
| -2 | 0.083333 |
| -1 | 0.125000 |
| 0 | 0.166667 |
| 1 | 0.166667 |
| 2 | 0.166667 |
| 3 | 0.125000 |
| 4 | 0.083333 |
| 5 | 0.041667 |
d4.mul_dist(d4)
| probs | |
|---|---|
| 1 | 0.0625 |
| 2 | 0.1250 |
| 3 | 0.1250 |
| 4 | 0.1875 |
| 6 | 0.1250 |
| 8 | 0.1250 |
| 9 | 0.0625 |
| 12 | 0.1250 |
| 16 | 0.0625 |
d4.div_dist(d4)
| probs | |
|---|---|
| 0.250000 | 0.0625 |
| 0.333333 | 0.0625 |
| 0.500000 | 0.1250 |
| 0.666667 | 0.0625 |
| 0.750000 | 0.0625 |
| 1.000000 | 0.2500 |
| 1.333333 | 0.0625 |
| 1.500000 | 0.0625 |
| 2.000000 | 0.1250 |
| 3.000000 | 0.0625 |
| 4.000000 | 0.0625 |
Comparison operators#
Pmf implements comparison operators that return probabilities.
You can compare a Pmf to a scalar:
d6.lt_dist(3)
0.3333333333333333
d4.ge_dist(2)
0.75
Or compare Pmf objects:
d4.gt_dist(d6)
0.25
d6.le_dist(d4)
0.41666666666666663
d4.eq_dist(d6)
0.16666666666666666
Interestingly, this way of comparing distributions is nontransitive.
A = Pmf.from_seq([2, 2, 4, 4, 9, 9])
B = Pmf.from_seq([1, 1, 6, 6, 8, 8])
C = Pmf.from_seq([3, 3, 5, 5, 7, 7])
A.gt_dist(B)
0.5555555555555556
B.gt_dist(C)
0.5555555555555556
C.gt_dist(A)
0.5555555555555556
Joint distributions#
For comments or questions about this section, see this issue.
Pmf.make_joint takes two Pmf objects and makes their joint distribution, assuming independence.
psource(Pmf.make_joint)
def make_joint(self, other, **options):
"""Make joint distribution (assuming independence).
Args:
other: Pmf
options: passed to Pmf constructor
Returns: new Pmf
"""
qs = pd.MultiIndex.from_product([self.qs, other.qs])
ps = np.multiply.outer(self.ps, other.ps).flatten()
return Pmf(ps, index=qs, **options)
d4 = Pmf.from_seq(range(1,5))
d4
| probs | |
|---|---|
| 1 | 0.25 |
| 2 | 0.25 |
| 3 | 0.25 |
| 4 | 0.25 |
d6 = Pmf.from_seq(range(1,7))
d6
| probs | |
|---|---|
| 1 | 0.166667 |
| 2 | 0.166667 |
| 3 | 0.166667 |
| 4 | 0.166667 |
| 5 | 0.166667 |
| 6 | 0.166667 |
joint = Pmf.make_joint(d4, d6)
joint
| probs | ||
|---|---|---|
| 1 | 1 | 0.041667 |
| 2 | 0.041667 | |
| 3 | 0.041667 | |
| 4 | 0.041667 | |
| 5 | 0.041667 | |
| 6 | 0.041667 | |
| 2 | 1 | 0.041667 |
| 2 | 0.041667 | |
| 3 | 0.041667 | |
| 4 | 0.041667 | |
| 5 | 0.041667 | |
| 6 | 0.041667 | |
| 3 | 1 | 0.041667 |
| 2 | 0.041667 | |
| 3 | 0.041667 | |
| 4 | 0.041667 | |
| 5 | 0.041667 | |
| 6 | 0.041667 | |
| 4 | 1 | 0.041667 |
| 2 | 0.041667 | |
| 3 | 0.041667 | |
| 4 | 0.041667 | |
| 5 | 0.041667 | |
| 6 | 0.041667 |
The result is a Pmf object that uses a MultiIndex to represent the values.
joint.index
MultiIndex([(1, 1),
(1, 2),
(1, 3),
(1, 4),
(1, 5),
(1, 6),
(2, 1),
(2, 2),
(2, 3),
(2, 4),
(2, 5),
(2, 6),
(3, 1),
(3, 2),
(3, 3),
(3, 4),
(3, 5),
(3, 6),
(4, 1),
(4, 2),
(4, 3),
(4, 4),
(4, 5),
(4, 6)],
)
If you ask for the qs, you get an array of pairs:
joint.qs
array([(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2),
(2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4),
(3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)],
dtype=object)
You can select elements using tuples:
joint[1,1]
0.041666666666666664
You can get unnnormalized conditional distributions by selecting on different axes:
Pmf(joint[1])
| probs | |
|---|---|
| 1 | 0.041667 |
| 2 | 0.041667 |
| 3 | 0.041667 |
| 4 | 0.041667 |
| 5 | 0.041667 |
| 6 | 0.041667 |
Pmf(joint.loc[:, 1])
| probs | |
|---|---|
| 1 | 0.041667 |
| 2 | 0.041667 |
| 3 | 0.041667 |
| 4 | 0.041667 |
But Pmf also provides conditional(i, val) which returns the conditional distribution where the value on level i is val.
psource(joint.conditional)
def conditional(self, i, val, name=None):
"""Gets the conditional distribution of the indicated variable.
Args:
i: index of the variable we're conditioning on
val: the value the ith variable has to have
name: string
Returns: Pmf
"""
pmf = Pmf(self.xs(key=val, level=i), copy=True, name=name)
pmf.normalize()
return pmf
joint.conditional(0, 1)
| probs | |
|---|---|
| 1 | 0.166667 |
| 2 | 0.166667 |
| 3 | 0.166667 |
| 4 | 0.166667 |
| 5 | 0.166667 |
| 6 | 0.166667 |
joint.conditional(1, 1)
| probs | |
|---|---|
| 1 | 0.25 |
| 2 | 0.25 |
| 3 | 0.25 |
| 4 | 0.25 |
It also provides marginal(i), which returns the marginal distribution along axis i
psource(Pmf.marginal)
def marginal(self, i, name=None):
"""Gets the marginal distribution of the indicated variable.
Args:
i: index of the variable we want
name: string
Returns: Pmf
"""
# The following is deprecated now
# return Pmf(self.sum(level=i))
# here's the new version
return Pmf(self.groupby(level=i).sum(), name=name)
joint.marginal(0)
| probs | |
|---|---|
| 1 | 0.25 |
| 2 | 0.25 |
| 3 | 0.25 |
| 4 | 0.25 |
joint.marginal(1)
| probs | |
|---|---|
| 1 | 0.166667 |
| 2 | 0.166667 |
| 3 | 0.166667 |
| 4 | 0.166667 |
| 5 | 0.166667 |
| 6 | 0.166667 |
Here are some ways of iterating through a joint distribution.
for q in joint.qs:
print(q)
(1, 1)
(1, 2)
(1, 3)
(1, 4)
(1, 5)
(1, 6)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(2, 5)
(2, 6)
(3, 1)
(3, 2)
(3, 3)
(3, 4)
(3, 5)
(3, 6)
(4, 1)
(4, 2)
(4, 3)
(4, 4)
(4, 5)
(4, 6)
for p in joint.ps:
print(p)
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
0.041666666666666664
for q, p in joint.items():
print(q, p)
(1, 1) 0.041666666666666664
(1, 2) 0.041666666666666664
(1, 3) 0.041666666666666664
(1, 4) 0.041666666666666664
(1, 5) 0.041666666666666664
(1, 6) 0.041666666666666664
(2, 1) 0.041666666666666664
(2, 2) 0.041666666666666664
(2, 3) 0.041666666666666664
(2, 4) 0.041666666666666664
(2, 5) 0.041666666666666664
(2, 6) 0.041666666666666664
(3, 1) 0.041666666666666664
(3, 2) 0.041666666666666664
(3, 3) 0.041666666666666664
(3, 4) 0.041666666666666664
(3, 5) 0.041666666666666664
(3, 6) 0.041666666666666664
(4, 1) 0.041666666666666664
(4, 2) 0.041666666666666664
(4, 3) 0.041666666666666664
(4, 4) 0.041666666666666664
(4, 5) 0.041666666666666664
(4, 6) 0.041666666666666664
for (q1, q2), p in joint.items():
print(q1, q2, p)
1 1 0.041666666666666664
1 2 0.041666666666666664
1 3 0.041666666666666664
1 4 0.041666666666666664
1 5 0.041666666666666664
1 6 0.041666666666666664
2 1 0.041666666666666664
2 2 0.041666666666666664
2 3 0.041666666666666664
2 4 0.041666666666666664
2 5 0.041666666666666664
2 6 0.041666666666666664
3 1 0.041666666666666664
3 2 0.041666666666666664
3 3 0.041666666666666664
3 4 0.041666666666666664
3 5 0.041666666666666664
3 6 0.041666666666666664
4 1 0.041666666666666664
4 2 0.041666666666666664
4 3 0.041666666666666664
4 4 0.041666666666666664
4 5 0.041666666666666664
4 6 0.041666666666666664
Copyright 2019 Allen Downey
BSD 3-clause license: https://opensource.org/licenses/BSD-3-Clause