Survey Data with Pandas and StatsModels

Survey Data with Pandas and StatsModels#

Tutorial for PyCon 2025

Allen B. Downey

Click here to run this notebook on Colab.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
Hide code cell content 
# Configure Matplotlib

plt.rcParams["figure.figsize"] = 7, 3.5
plt.rcParams["figure.dpi"] = 75
plt.rcParams["axes.titlelocation"] = "left"
plt.rcParams["axes.spines.top"] = False
plt.rcParams["axes.spines.bottom"] = False
plt.rcParams["axes.spines.left"] = False
plt.rcParams["axes.spines.right"] = False

from os.path import basename, exists

def download(url):
    filename = basename(url)
    if not exists(filename):
        from urllib.request import urlretrieve
        local, _ = urlretrieve(url, filename)
        print('Downloaded ' + local)

def decorate(**options):
    """Decorate the current axes.

    Call decorate with keyword arguments like
    decorate(title='Title',
             xlabel='x',
             ylabel='y')

    The keyword arguments can be any of the axis properties
    https://matplotlib.org/api/axes_api.html
    """
    legend = options.pop("legend", True)
    loc = options.pop("loc", "best")

    # Pass options to Axis.set
    ax = plt.gca()
    ax.set(**options)

    # Add a legend if there are any labeled elements
    handles, labels = ax.get_legend_handles_labels()
    if handles and legend:
        ax.legend(handles, labels, loc=loc)

    # Tight layout is generally a good idea
    plt.tight_layout()

Data#

We will use data from the General Social Survey (GSS). The raw dataset is big, so I’ve prepared an extract, which the following cell downloads. The code to generate the extract is in this notebook.

# This dataset is prepared in the GssExtract repository

DATA_PATH = "https://github.com/AllenDowney/GssExtract/raw/main/data/interim/"

filename = "gss_extract_pacs_workshop.hdf"
download(DATA_PATH + filename)
Hide code cell content 
# Solution

gss = pd.read_hdf(filename, "gss")
gss.shape

(72390, 29)
Hide code cell content 
# Solution

gss.head()
age attend ballot class cohort degree educ fair fear goodlife ... region relig rincome satfin satjob sex srcbelt trust wtssall year
0 24.0 1.0 NaN 3.0 1948.0 3.0 16.0 2.0 NaN NaN ... 1 1.0 NaN 1.0 NaN 1.0 5.0 1.0 1.3339 1972
1 33.0 2.0 NaN 2.0 1939.0 0.0 10.0 2.0 NaN NaN ... 1 2.0 NaN 3.0 2.0 1.0 1.0 1.0 0.8893 1972
2 40.0 8.0 NaN 2.0 1932.0 1.0 12.0 2.0 NaN NaN ... 1 5.0 NaN 1.0 NaN 2.0 3.0 2.0 1.3339 1972
3 24.0 2.0 NaN 2.0 1948.0 1.0 12.0 1.0 NaN NaN ... 9 2.0 NaN 2.0 NaN 1.0 3.0 2.0 1.7786 1972
4 21.0 7.0 NaN 3.0 1951.0 1.0 12.0 1.0 NaN NaN ... 9 1.0 NaN 1.0 NaN 2.0 2.0 NaN 1.7786 1972

5 rows × 29 columns

Hide code cell content 
# Solution

gss.columns

Index(['age', 'attend', 'ballot', 'class', 'cohort', 'degree', 'educ', 'fair',
       'fear', 'goodlife', 'hapmar', 'happy', 'health', 'helpful', 'id',
       'life', 'partyid', 'polviews', 'race', 'region', 'relig', 'rincome',
       'satfin', 'satjob', 'sex', 'srcbelt', 'trust', 'wtssall', 'year'],
      dtype='object')
Hide code cell content 
# Solution

gss.isna().mean().sort_values()

id          0.000000
year        0.000000
wtssall     0.000000
region      0.000000
srcbelt     0.000718
race        0.001796
sex         0.002086
degree      0.002942
educ        0.004338
cohort      0.005567
relig       0.007087
partyid     0.007294
attend      0.009711
age         0.010416
class       0.048501
satfin      0.063641
happy       0.065106
polviews    0.131620
health      0.236552
satjob      0.265064
ballot      0.302183
fear        0.365147
life        0.386669
rincome     0.402086
trust       0.410982
helpful     0.414090
fair        0.415665
hapmar      0.468241
goodlife    0.631924
dtype: float64

Distributions#

We’ll see two ways to describe distributions: value counts and KDE.

And for joint distributions, we’ll use a cross tabulation.

def value_counts(seq, **options):
    """Make a series of values and the number of times they appear.

    Args:
        seq: sequence

    returns: Pandas Series
    """
    return pd.Series(seq).value_counts(**options).sort_index()
Hide code cell content 
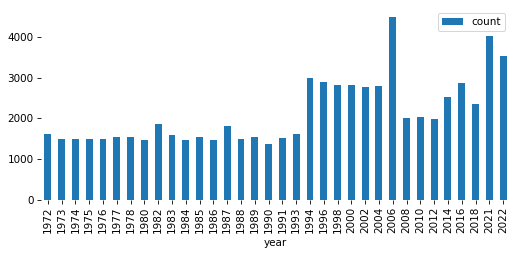
# Solution

pmf = value_counts(gss['year'])
pmf.plot(kind='bar')
decorate()
_images/83c89e5a603958cf5bd11666ed654753a69305b9953aac0a1e0e48af4288e99e.png
Hide code cell content 
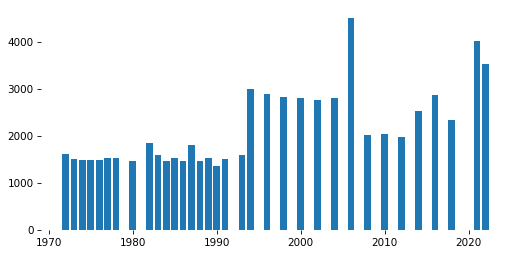
# Solution

x, y = pmf.index, pmf.values
plt.bar(x, y)
decorate()
_images/eb69ddb3428934054c96b5e7b6480257cab5a54e4be46d71d0faf417aaa2e6f9.png
Hide code cell content 
# Solution

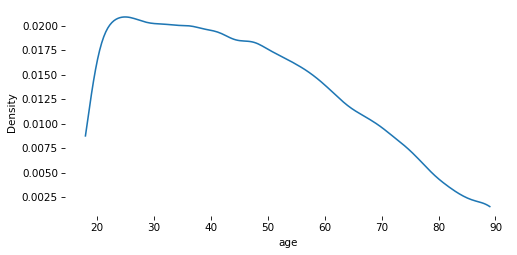
gss['age'].describe()

count    71636.000000
mean        44.985943
std         17.201666
min         18.000000
25%         30.000000
50%         43.000000
75%         58.000000
max         89.000000
Name: age, dtype: float64
Hide code cell content 
# Solution

sns.kdeplot(gss['age'], cut=0)
decorate()
_images/d78b8005d00037fb3a0d0580e1846fd3e6d0d4db93c0711aa6d99fab879b5baa.png
Hide code cell content 
# Solution

gss['cohort'].describe()

count    71987.000000
mean      1991.908095
std        561.717010
min       1883.000000
25%       1938.000000
50%       1954.000000
75%       1968.000000
max       9999.000000
Name: cohort, dtype: float64
Hide code cell content 
# Solution

gss['cohort'] = gss['cohort'].replace(9999, np.nan)

Exercise#

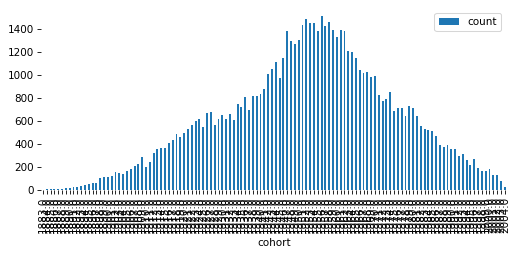
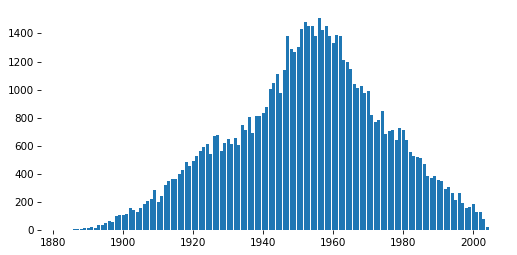
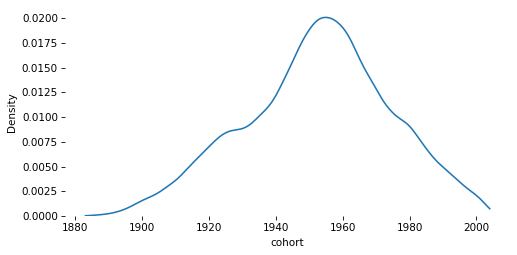
Use value_counts to plot the distribution of cohort as a bar plot. Then use sns.kdeplot to show the same distribution as a continuous quantity.

Hide code cell content 
# Solution

pmf = value_counts(gss['cohort'])
pmf.plot(kind='bar')
decorate(ylabel='Count')
_images/1372a512a5859be14cac79bd3c790b38f180893980f42e242acd9f180f35cb2b.png
Hide code cell content 
# Solution

x, y = pmf.index, pmf.values
plt.bar(x, y)
decorate(ylabel='Count')
_images/2d2b5505210a7e7af75e9e854737f8b9a82b17ca5badfa71a758af547e265c27.png
Hide code cell content 
# Solution

sns.kdeplot(gss['cohort'], cut=0)
decorate()
_images/5b8a241bcf300a98efb59cf601923825638b6929f3ac54efa292be5de39b8fc5.png

Cross tabulation#

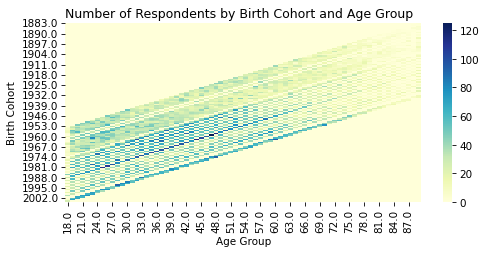
Cross tabulation is a way to represent the joint distribution of two variables.

Hide code cell content 
# Solution

xtab = pd.crosstab(gss['cohort'], gss['age'])
xtab
age 18.0 19.0 20.0 21.0 22.0 23.0 24.0 25.0 26.0 27.0 ... 80.0 81.0 82.0 83.0 84.0 85.0 86.0 87.0 88.0 89.0
cohort
1883.0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 1
1884.0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 1 1
1885.0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 5
1886.0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 4 4
1887.0 0 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 2 1 0 1 4
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2000.0 36 0 0 71 77 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
2001.0 0 0 68 63 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
2002.0 0 59 69 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
2003.0 7 70 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0
2004.0 25 0 0 0 0 0 0 0 0 0 ... 0 0 0 0 0 0 0 0 0 0

122 rows × 72 columns

Hide code cell content 
# Solution

sns.heatmap(
    xtab,
    cmap="YlGnBu",
)

plt.title("Number of Respondents by Birth Cohort and Age Group")
plt.xlabel("Age Group")
plt.ylabel("Birth Cohort")
decorate()
_images/26f48537afb36755a3bee5871bb5ca08f3e069b4ed5703b9e6001bba98bf7fe3.png

Target variable#

I’ve selected four variables you might want to work with. Whichever one you choose, put its cell last.

# https://gssdataexplorer.norc.org/variables/434/vshow

varname = 'happy'

question = """Taken all together, how would you say things are these days--
would you say that you are very happy, pretty happy, or not too happy?
"""

responses = ['Very happy', "Happy", 'Not too happy']

ylabel = "Percent saying 'very happy'"

# https://gssdataexplorer.norc.org/variables/439/vshow

varname = 'helpful'

question = """Would you say that most of the time people try to be helpful,
or that they are mostly just looking out for themselves?
"""

responses = ['Helpful', 'Look out\nfor themselves', 'Depends']

ylabel = "Percent saying 'helpful'"

# https://gssdataexplorer.norc.org/variables/440/vshow

varname = 'fair'

question = """Do you think most people would try to take advantage of you 
if they got a chance, or would they try to be fair?
"""

# notice that the negative response is first here!
responses = ['Take advantage', 'Fair', 'Depends']

ylabel = "Percent saying 'fair'"

# https://gssdataexplorer.norc.org/variables/441/vshow

varname = 'trust'

question = """Generally speaking, would you say that most people can be trusted
or that you can't be too careful in dealing with people?
"""

responses = ['Trusted', "Can't be\ntoo careful", 'Depends']

ylabel = "Percent saying 'trusted'"
Hide code cell content 
# Solution

column = gss[varname]
column

0        1.0
1        1.0
2        2.0
3        2.0
4        NaN
        ... 
72385    2.0
72386    2.0
72387    NaN
72388    NaN
72389    1.0
Name: trust, Length: 72390, dtype: float64
Hide code cell content 
# Solution

value_counts(column, dropna=False)

trust
1.0    15783
2.0    24890
3.0     1966
NaN    29751
Name: count, dtype: int64
Hide code cell content 
# Solution

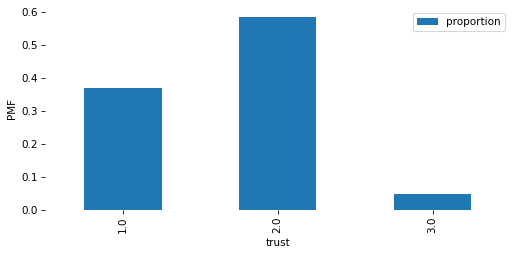
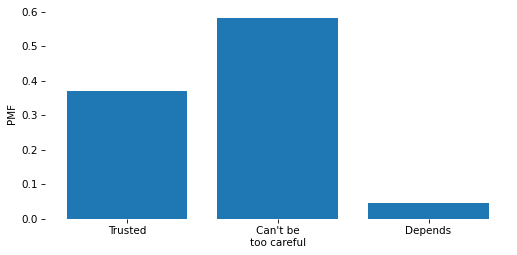
pmf = value_counts(column, normalize=True)
pmf

trust
1.0    0.370154
2.0    0.583738
3.0    0.046108
Name: proportion, dtype: float64
Hide code cell content 
# Solution

pmf.plot(kind='bar')
decorate(ylabel='PMF')
_images/e7ecb0b1a0b913644baceec9cbc787cc09a213ff84533c93d7789f05de31d24d.png
Hide code cell content 
# Solution

plt.bar(pmf.index, pmf)
plt.xticks(pmf.index, responses)

decorate(ylabel='PMF')
_images/895da4aa114da4e731b51eff6ac819a834589a39229356c4d57b0bce99baf90f.png

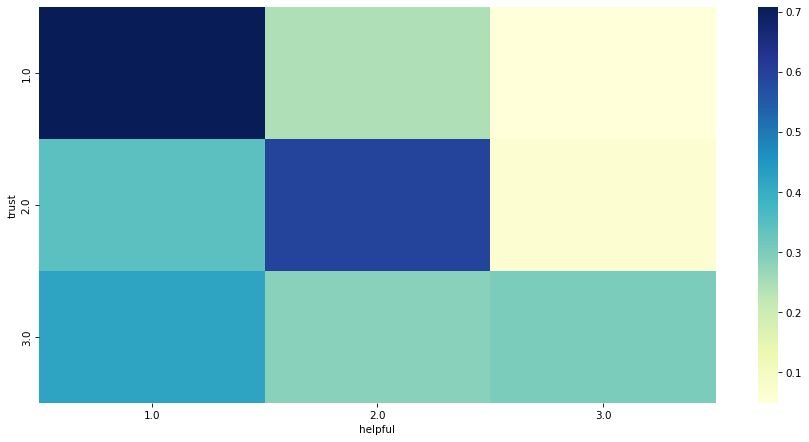
Exercise#

Do you think people who say “trust” are also more likely to say “helpful”? To find out, make a cross tabulation of trust and helpful. Consider using normalize='index'. Make a heatmap that shows this joint distribution. What relationships can you see in the responses?

Hide code cell content 
# Solution

xtab = pd.crosstab(gss['trust'], gss['helpful'], normalize='index')
xtab
helpful 1.0 2.0 3.0
trust
1.0 0.707773 0.243133 0.049094
2.0 0.340947 0.592560 0.066493
3.0 0.417197 0.283970 0.298832
Hide code cell content 
# Solution

plt.figure(figsize=(12, 6))
sns.heatmap(
    xtab,
    cmap="YlGnBu",
)

decorate(xlabel='helpful', ylabel='trust')
_images/6d8d0d816fbd95c463bc2b39af912d0e7717c1f47c698343fa32fc9703ab611a.png

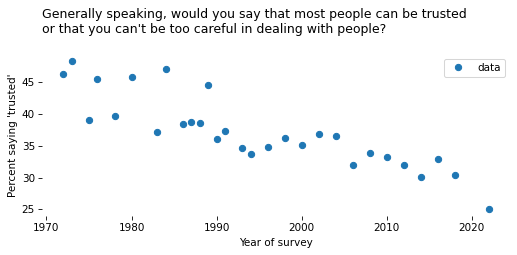
Time Series#

To see how responses have changed over time, we’ll use cross tabulation again.

Hide code cell content 
# Solution

xtab = pd.crosstab(gss["year"], gss[varname], normalize='index')
xtab.head()
trust 1.0 2.0 3.0
year
1972 0.463551 0.490343 0.046106
1973 0.483656 0.495664 0.020680
1975 0.391099 0.564396 0.044504
1976 0.455518 0.513043 0.031438
1978 0.396597 0.549738 0.053665
Hide code cell content 
# Solution

gss72 = gss.query('year == 1972')
gss72.shape

(1613, 29)
Hide code cell content 
# Solution

pmf72 = value_counts(gss72[varname], normalize=True)
pmf72

trust
1.0    0.463551
2.0    0.490343
3.0    0.046106
Name: proportion, dtype: float64
Hide code cell content 
# Solution

time_series = xtab[1] * 100
time_series.name = "data"
Hide code cell content 
# Solution

time_series.plot(style='o')
decorate(
    xlabel="Year of survey",
    ylabel=ylabel,
    title=question,
)
_images/2fd9bee674bb0be6a8d82c1474c9e4ddb379e4e5a9d960fe8148cf652e720daa.png

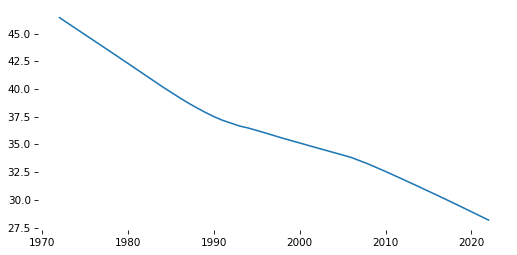
Smoothing#

To smooth the time series, we’ll use LOWESS (locally weighted scatterplot smoothing).

Hide code cell content 
# Solution

x = time_series.index.to_numpy()
y = time_series.to_numpy()
Hide code cell content 
# Solution

from statsmodels.nonparametric.smoothers_lowess import lowess

smooth_array = lowess(y, x)
Hide code cell content 
# Solution

index, data = np.transpose(smooth_array)
smooth_series = pd.Series(data, index=index)
Hide code cell content 
# Solution

smooth_series.plot()
decorate()
_images/452290539f10c28f25597f2951ba31440985798585d248a74adaaad4199f3e9d.png 
def make_lowess(series, frac=0.5):
    """Use LOWESS to compute a smooth line.

    series: pd.Series

    returns: pd.Series
    """
    y = series.to_numpy()
    x = series.index.to_numpy()

    smooth_array = lowess(y, x, frac)
    index, data = np.transpose(smooth_array)

    return pd.Series(data, index=index)

Exercise#

Use this function to make smooth_series. Plot the result along with time_series.

Hide code cell content 
# Solution

smooth_series = make_lowess(time_series)
Hide code cell content 
# Solution

time_series.plot(style='o', alpha=0.5)
smooth_series.plot(label='smoothed', color='C0')

decorate(
    xlabel="Year of survey",
    ylabel=ylabel,
    title=question,
)
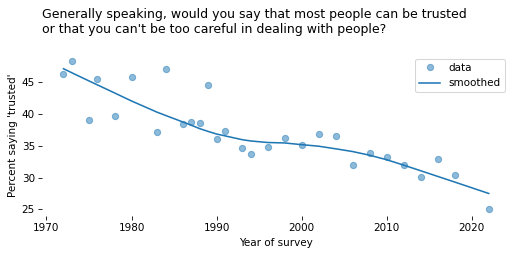
_images/6ca7290a2c3bd5d10d73d3a0b7923d400db29b2f225f48e00a70ee8af1ade892.png

Binary series#

It will be useful to convert the responses to a binary variable represented with 0s and 1s.

Hide code cell content 
# Solution

# tempting but wrong

gss['y'] = gss[varname] == 1
value_counts(gss['y'], dropna=False)

y
False    56607
True     15783
Name: count, dtype: int64
Hide code cell content 
# Solution

gss['y'] = np.where(gss[varname].notna(), gss[varname] == 1, np.nan)
value_counts(gss['y'], dropna=False)

y
0.0    26856
1.0    15783
NaN    29751
Name: count, dtype: int64
Hide code cell content 
# Solution

# Reminder: this needs to be updated depending on the target variable

gss['y'] = gss[varname].replace([1, 2, 3], [1, 0, 0])
value_counts(gss['y'], dropna=False)

y
0.0    26856
1.0    15783
NaN    29751
Name: count, dtype: int64

Pivot tables#

Now we’ll use a pivot table to put respondents in groups and see how the responses have changed over time.

polviews_map = {
    1: 'Liberal',
    2: 'Liberal',
    3: 'Liberal',
    4: 'Moderate',
    5: 'Conservative',
    6: 'Conservative',
    7: 'Conservative',
}
Hide code cell content 
# Solution

gss['polviews3'] = gss['polviews'].replace(polviews_map)
Hide code cell content 
# Solution

value_counts(gss['polviews3'], dropna=False)

polviews3
Conservative    21580
Liberal         17370
Moderate        23912
NaN              9528
Name: count, dtype: int64
Hide code cell content 
# Solution

table = gss.pivot_table(
    index='year', columns='polviews3', values='y', aggfunc='mean'
) * 100
table.head()
polviews3 Conservative Liberal Moderate
year
1975 41.891892 39.192399 38.733706
1976 49.590164 45.961003 44.561404
1978 42.699115 43.262411 37.347295
1980 47.609562 45.896657 46.204620
1983 41.935484 31.914894 39.240506
Hide code cell content 
# Solution

table.plot(style='.:')
decorate()
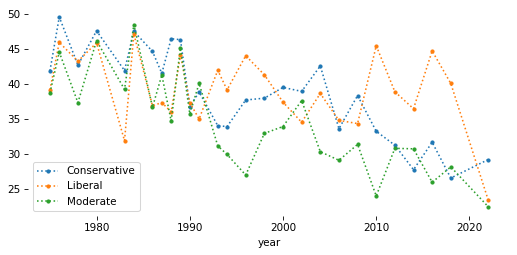
_images/d6b30712b6529135b5efe0387c45c43cc16817eae1ca2237e32826c839c0ebc5.png

Better colors#

We’ll select colors from a Seaborn color palette.

Hide code cell content 
# Solution

muted = sns.color_palette('muted', 5)
sns.palplot(muted)
_images/94854b22037f74f36a5e0187dc3f20d942ad047ddb5af82360b9aeb6559349f9.png
Hide code cell content 
# Solution

color_map = {
    'Conservative': muted[3], 
    'Moderate': muted[4], 
    'Liberal': muted[0]
}

Exercise#

Loop through the groups in color_map. For each one, extract a column from table and plot the data points; then plot a smooth line.

Hide code cell content 
# Solution

for group in color_map:
    series = table[group]
    color = color_map[group]
    series.plot(style='o', label='', color=color, alpha=0.3)
    smooth = make_lowess(series)
    smooth.plot(label=group, color=color)

decorate(
    xlabel='Year',
    ylabel=ylabel,
    title=question,
)
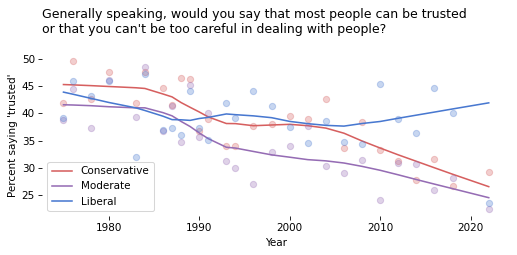
_images/2a78db011bcde07e5b872817ee820731b22708662a933bf2fe76ecd17ecb7453.png

Groupby#

Now that we have y as a binary variable, we have another way to compute the time series and the pivot table. There are pros and cons of each method.

Hide code cell content 
# Solution

valid = gss.dropna(subset=['y'])
Hide code cell content 
# Solution

time_series2 = valid.groupby('year')['y'].mean() * 100
assert np.allclose(time_series, time_series2)
Hide code cell content 
# Solution

table2 = valid.groupby(['year', 'polviews3'])['y'].mean().unstack() * 100
assert np.allclose(table, table2)

Logistic regression#

We’ll use logistic regression to model changes over time.

Hide code cell content 
# Solution

year_shift = gss['year'].median()
gss['x'] = gss['year'] - year_shift
Hide code cell content 
# Solution

subset = gss.dropna(subset=['y', 'x'])
Hide code cell content 
# Solution

import statsmodels.formula.api as smf

formula = 'y ~ x + I(x**2)'

model = smf.logit(formula, data=subset).fit(disp=False)
model.params

Intercept   -0.588941
x           -0.014565
I(x ** 2)    0.000057
dtype: float64
Hide code cell content 
# Solution

year_range = np.arange(1972, 2026)

pred_df = pd.DataFrame(dict(x=year_range - year_shift))

pred_series = model.predict(pred_df) * 100
pred_series.index = year_range
Hide code cell content 
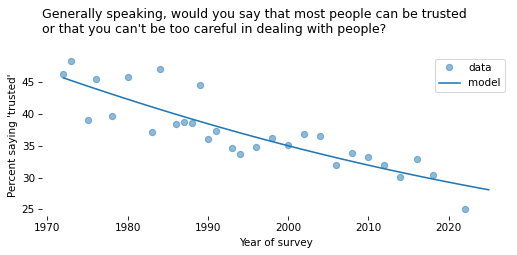
# Solution

time_series.plot(style='o', alpha=0.5)
pred_series.plot(label='model', color='C0')

decorate(
    xlabel="Year of survey",
    ylabel=ylabel,
    title=question,
)
_images/40715ac8640363b74f01322ff37d266607fb2b312fb69bdce9ca09e8af207728.png 
def fit_model(data, x_range, x_shift):
    formula = 'y ~ x + I(x**2)'
    model = smf.logit(formula, data=data).fit(disp=False)
    
    pred_df = pd.DataFrame(dict(x=x_range - x_shift))
    pred = model.predict(pred_df) * 100
    pred.index = x_range
    pred.name = 'model'

    return pred
Hide code cell content 
# Solution

pred_series2 = fit_model(subset, year_range, year_shift)
assert np.allclose(pred_series, pred_series2)

Exercise#

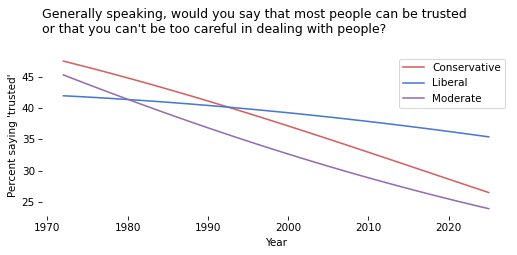
Use subset.groupby('polviews3') to loop through the groups. For each one, use fit_model to generate and plot a “prediction” for the group.

Hide code cell content 
# Solution

for name, group in subset.groupby('polviews3'):
    pred_series = fit_model(group, year_range, year_shift)
    pred_series.plot(label=name, color=color_map[name])
    
decorate(
    xlabel='Year',
    ylabel=ylabel,
    title=question,
)
_images/1ff755a37e2b218560af8f91ebc976d92c955b66b26fcfc22403a6dd0dad5800.png

Group by cohort#

Now let’s group respondents by decade of birth and see how each cohort changes over time.

def round_into_bins(series, bin_width, low=0, high=None):
    """Rounds values down to the bin they belong in.

    series: pd.Series
    bin_width: number, width of the bins

    returns: Series of bin values (with NaN preserved)
    """
    if high is None:
        high = series.max()

    bins = np.arange(low, high + bin_width, bin_width)
    indices = np.digitize(series, bins)
    result = pd.Series(bins[indices - 1], index=series.index, dtype='float')

    result[series.isna()] = np.nan
    return result
Hide code cell content 
# Solution

gss["cohort10"] = round_into_bins(gss["cohort"], 10, 1880)
value_counts(gss["cohort10"], dropna=False)

cohort10
1880.0       45
1890.0      501
1900.0     1722
1910.0     3616
1920.0     5862
1930.0     7115
1940.0    10925
1950.0    14273
1960.0    11699
1970.0     7681
1980.0     5088
1990.0     2563
2000.0      545
NaN         755
Name: count, dtype: int64
Hide code cell content 
# Solution

cohort_df = gss.query("cohort10 == 1940").dropna(subset=['y', 'x'])
cohort_df.shape

(6825, 33)
Hide code cell content 
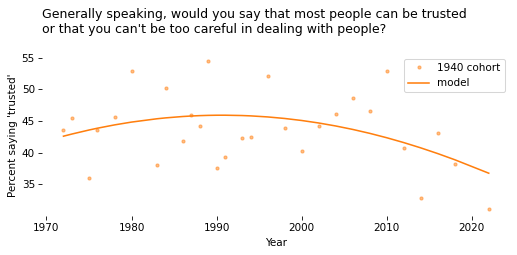
# Solution

cohort_series = cohort_df.groupby('year')['y'].mean() * 100
cohort_series.name = '1940 cohort'
Hide code cell content 
# Solution

x_range = cohort_series.index
pred_series = fit_model(cohort_df, x_range, year_shift)
Hide code cell content 
# Solution

cohort_series.plot(style='.', color='C1', alpha=0.5)
pred_series.plot(color='C1')

decorate(
    xlabel="Year",
    ylabel=ylabel,
    title=question,
)
_images/3b946a585b45e0be26a39b730edd3fc9a3b5986eb6e639042ac59ec71914036a.png

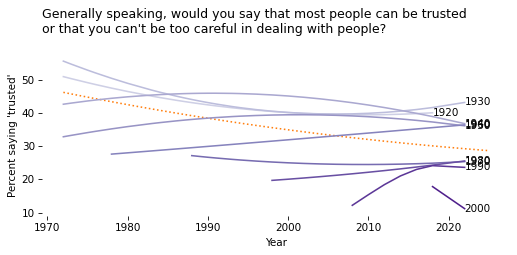
All the Cohorts#

Now let’s compare cohorts. The following function encapsulates the steps from the previous section.

def plot_cohort(df, cohort, color='C0'):
    cohort_df = df.query("cohort10 == @cohort").dropna(subset=['y', 'x'])

    cohort_series = cohort_df.groupby('year')['y'].mean() * 100

    year_range = cohort_series.index

    pred_series = fit_model(cohort_df, year_range, year_shift)
    x, y = pred_series.index[-1], pred_series.values[-1]
    plt.text(x, y, cohort, ha='left', va='center')

    pred_series.plot(label=cohort, color=color)
Hide code cell content 
# Solution

first, last = 1920, 2000
subset = gss.query("@first <= cohort <= @last" )
subset.shape

(65390, 33)
Hide code cell content 
# Solution

pred_all = fit_model(subset, year_range, year_shift)
Hide code cell content 
# Solution

cohorts = np.sort(subset['cohort10'].unique().astype(int))
cohorts

array([1920, 1930, 1940, 1950, 1960, 1970, 1980, 1990, 2000])
Hide code cell content 
# Solution

cmap = plt.get_cmap('Purples')

colors = [cmap(x) for x in np.linspace(0.3, 0.9, len(cohorts))]

Exercise#

Plot pred_all. Then loop through cohorts and colors, and call plot_cohort for each group.

Depending on which target variable you chose, you might get a warning from StatsModels.

Hide code cell content 
# Solution

pred_all.plot(ls=':', color='C1')

for cohort, color in zip(cohorts, colors):
    plot_cohort(gss, cohort, color)
    
decorate(
    xlabel="Year",
    ylabel=ylabel,
    title=question,
    legend=False
)

/home/downey/miniconda3/envs/SurveyDataPandas/lib/python3.13/site-packages/statsmodels/base/model.py:607: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
  warnings.warn("Maximum Likelihood optimization failed to "
_images/ffbebe44b0cedcb61a7658129951aa063560ac23c6f1d2524d8a48badac9207d.png

Simpson’s Paradox#

The composition of the population changes over time.

Hide code cell content 
# Solution

xtab_cohort = pd.crosstab(gss["cohort10"], gss["year"], normalize="columns")
xtab_cohort.head()
year 1972 1973 1974 1975 1976 1977 1978 1980 1982 1983 ... 2004 2006 2008 2010 2012 2014 2016 2018 2021 2022
cohort10
1880.0 0.003113 0.003995 0.008108 0.006739 0.004692 0.000000 0.003277 0.000000 0.000000 0.000000 ... 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.0 0.0
1890.0 0.047945 0.038615 0.029730 0.037062 0.047587 0.027613 0.028834 0.017088 0.018929 0.005013 ... 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.0 0.0
1900.0 0.110212 0.099201 0.129730 0.082210 0.070375 0.091387 0.083224 0.059467 0.051379 0.038221 ... 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000 0.0 0.0
1910.0 0.152553 0.158455 0.131081 0.130728 0.144772 0.125575 0.105505 0.124402 0.103840 0.093358 ... 0.015714 0.007562 0.007944 0.000000 0.000000 0.000000 0.000000 0.000000 0.0 0.0
1920.0 0.224782 0.180426 0.193243 0.187332 0.159517 0.184747 0.152687 0.160629 0.149270 0.137218 ... 0.038929 0.040036 0.038232 0.035294 0.025381 0.014235 0.009807 0.008576 0.0 0.0

5 rows × 34 columns

Hide code cell content 
# Solution

xtab_cohort[1972].plot(label="1972")
xtab_cohort[1998].plot(label="1998")
xtab_cohort[2022].plot(label="2022")

decorate(xlabel="Year of birth", ylabel="Fraction of sample")
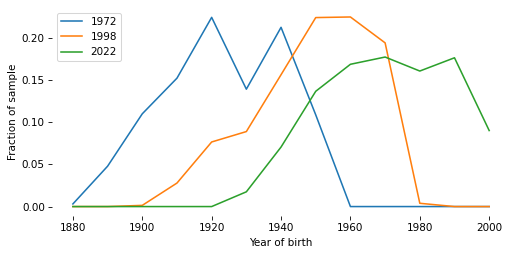
_images/b42fa5779eb09acc78349cb22aab965f7d09390c72d209d14cda6ba47a587914.png

Sampling weights#

The GSS uses stratified sampling, so some respondents represent more people in the population than others. We can use resampling to correct for stratified sampling.

Hide code cell content 
# Solution

gss['wtssall'].describe()

count    72390.000000
mean         1.303960
std          0.889990
min          0.113721
25%          0.918400
50%          1.062700
75%          1.547800
max         14.272462
Name: wtssall, dtype: float64
Hide code cell content 
# Solution

gss.groupby('year')['wtssall'].describe()
count mean std min 25% 50% 75% max
year
1972 1613.0 1.146481 0.486191 0.444600 0.889300 0.889300 1.333900 3.557100
1973 1504.0 1.130645 0.417802 0.457200 0.914500 0.914500 1.371700 2.743500
1974 1484.0 1.160032 0.443681 0.466000 0.932000 0.932000 1.397900 3.727900
1975 1490.0 1.140258 0.466167 0.466000 0.932000 0.932000 1.397900 3.261900
1976 1499.0 1.147392 0.459938 0.485400 0.970900 0.970900 1.456300 3.398100
1977 1530.0 1.161231 0.458057 0.494100 0.988100 0.988100 1.482200 2.964400
1978 1532.0 1.148797 0.448502 0.506300 1.012700 1.012700 1.519000 3.038000
1980 1468.0 1.168663 0.486058 0.511200 1.022500 1.022500 1.533700 3.578700
1982 1860.0 1.189170 0.513264 0.506400 1.031900 1.031900 1.547800 4.127500
1983 1599.0 1.174535 0.489286 0.505800 1.011600 1.011600 1.517500 3.540700
1984 1473.0 1.163876 0.473032 0.516500 1.033100 1.033100 1.549600 3.615700
1985 1534.0 1.158889 0.463941 0.518100 1.036300 1.036300 1.554400 3.626900
1986 1470.0 1.164447 0.467082 0.503600 1.007200 1.007200 1.510800 3.021600
1987 1819.0 1.186371 0.499286 0.505200 1.010400 1.010400 1.515500 3.536200
1988 1481.0 1.163860 0.463531 0.531300 1.062700 1.062700 1.062700 3.719400
1989 1537.0 1.184300 0.504330 0.510700 1.021500 1.021500 1.532200 3.575100
1990 1372.0 1.161439 0.489095 0.531300 1.062700 1.062700 1.062700 3.188100
1991 1517.0 1.174147 0.478842 0.531100 1.062100 1.062100 1.593200 3.717500
1993 1606.0 1.169310 0.448682 0.528500 1.057100 1.057100 1.585600 3.699800
1994 2992.0 1.166058 0.457253 0.541200 1.082500 1.082500 1.082500 3.247500
1996 2904.0 1.181024 0.479229 0.543200 1.086400 1.086400 1.086400 3.259100
1998 2832.0 1.177809 0.462729 0.550100 1.100100 1.100100 1.100100 3.850400
2000 2817.0 1.165950 0.453726 0.549300 1.098500 1.098500 1.098500 3.295600
2002 2765.0 1.198505 0.507470 0.557800 1.115600 1.115600 1.115600 2.788900
2004 2812.0 1.299424 0.762699 0.459200 0.918400 0.961700 1.836800 6.428700
2006 4510.0 1.360152 0.841060 0.429700 0.859300 0.954800 1.909600 5.728800
2008 2023.0 1.425750 0.911863 0.437745 0.875490 1.067670 2.135340 6.406021
2010 2044.0 1.313222 0.726111 0.463128 0.926255 0.926255 1.684101 4.210252
2012 1974.0 1.366495 0.884637 0.411898 0.823796 1.235694 1.747975 8.739876
2014 2538.0 1.273430 0.674193 0.448002 0.896003 1.344005 1.380591 5.376020
2016 2867.0 1.227412 0.607020 0.391825 0.956994 0.956994 1.564363 4.306471
2018 2348.0 1.382192 0.936160 0.471499 0.942997 0.942997 1.414496 5.897420
2021 4032.0 1.551637 1.175611 0.227357 0.790829 1.195842 1.869697 7.557038
2022 3544.0 2.551821 2.489079 0.113721 0.714314 1.781121 3.529911 14.272462 
def resample_by_year(df, column='wtssall'):
    """Resample rows within each year using weighted sampling.

    df: DataFrame
    column: string name of weight variable

    returns: DataFrame
    """
    grouped = df.groupby('year')
    samples = [group.sample(n=len(group), replace=True, weights=group[column])
               for _, group in grouped]
    sample = pd.concat(samples, ignore_index=True)
    return sample
Hide code cell content 
# Solution

sample = resample_by_year(gss)
Hide code cell content 
# Solution

sample['y'].mean()

np.float64(0.36038778568752344)
Hide code cell content 
# Solution

gss['y'].mean()

np.float64(0.3701540842890312)
Hide code cell content 
# Solution

weighted_mean = np.average(valid['y'], weights=valid['wtssall'])

Copyright 2025 Allen Downey

The code in this notebook is under the MIT license.

Contents